CRF损失函数与Viterbi算法

CRF考虑到了输出层面的关联性，如下图所示：

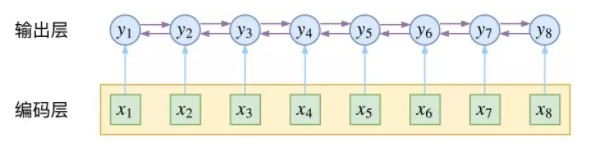
损失函数

时间步 $t$ 输出的标签值由两部分组成：

发射分数：$ h(y_t;X) $
转移分数：$ g(y_t;y_{t-1}) $

一条路径标识为 $y_1, y_2, \dots , y_n$ 的概率为：

$P(y_1, y_2, \dots, y_n | X) = \frac{1}{Z(X)} e^{h(y_1;x)+\sum_{i=2}^{n}g(y_i;y_{i-1})+h(y_i;X)}$

其中 $Z(X)$ 为归一化因子。在 CRF 模型中，由于我们只考虑了临近标签的联系（马尔可夫假设），因此我们可以递归地算出归一化因子，这使得原来是指数级的计算量降低为线性级别。

具体来说，我们将计算到时刻 $t$ 的归一化因子记为 $Z_t$，并将它分为 $k$ 个部分：

$Z_t = Z_t^1 + Z_t^2 + \cdots + Z_t^k$

上式分别是截止到当前时刻 $t$ 中、以标签 $1,2,\cdots, k$ 为终点的所有路径的得分指数和。那么，我们可以递归地计算：

$\begin{array}{l} Z_{t+1}^{(1)}=\left(Z_{t}^{(1)} G_{11}+Z_{t}^{(2)} G_{21}+\cdots+Z_{t}^{(k)} G_{k 1}\right) H_{t+1}(1 \mid X) \\ Z_{t+1}^{(2)}=\left(Z_{t}^{(1)} G_{12}+Z_{t}^{(2)} G_{22}+\cdots+Z_{t}^{(k)} G_{k 2}\right) H_{t+1}(2 \mid X) \\ \vdots \\ Z_{t+1}^{(k)}=\left(Z_{i}^{(1)} G_{1 k}+Z_{t}^{(2)} G_{2 k}+\cdots+Z_{t}^{(k)} G_{k k}\right) H_{t+1}(k \mid X) \end{array}$

其中$G_{ij} = e^{g(y_j;y_i)}, H(y_{t+1}|X)=e^{h(y_{t+1}|X)}$，上式简写成矩阵形式为：

$Z_{t+1} = Z_tG \otimes H_{t+1}$

为了符合损失函数的含义，将其定义为：

$Loss = -logP(y_1, y_2, \dots, y_n | X)$

viterbi 算法

有了损失函数后，就可以通过反向传播结合梯度下降来求解最优参数。

序列标注的目标是找出一条概率最高的路径。假设整个网络的宽度为 $k$，网络长度为 $N$ ，按照穷举法求最佳路径的时间复杂度为 $O(k^N)$，但CRF采用了马尔可夫假设，因此可以使用动态规划来求解，时间复杂度优化到 $O(N \times k^2)$。

具体示例可见：如何通俗地讲解 viterbi 算法？

损失函数

viterbi 算法

参考