FM 是搜广推里最经典的算法，这里记录一下原理与公式推导：

FM

参数数量和时间复杂度优化

当我们使用一阶原始特征和二阶组合特征来刻画样本的时候，会得到如下式子：

$\hat{y}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} w_{i j} x_{i} x_{j}$

$x_i$ 和 $x_j$ 分别表示两个不同的特征取值，对于 $n$ 维的特征来说，这样的二阶组合特征一共有 $\frac{n(n-1)}{2}$ 种，也就意味着我们需要同样数量的权重参数。但是由于现实场景中的特征是高维稀疏的，导致 $n$ 非常大，比如上百万，这里两两特征组合的特征量级 $C_n^2$ ，所带来的参数量就是一个天文数字。对于一个上百亿甚至更多参数空间的模型来说，我们需要海量训练样本才可以保证完全收敛。这是非常困难的。

FM解决这个问题的方法非常简单，它不再是简单地为交叉之后的特征对设置参数，而是设置了一种计算特征参数的方法。

FM模型引入了新的矩阵 $V$ ，它是一个 $n \times k$ 的二维矩阵。这里的 $k$ 是超参，一般不会很大，比如16、32之类。对于特征每一个维度 $x_i$ ，我们都可以找到一个表示向量 $v_i \in R^k$ 。从NLP的角度来说，就是为每个特征学习一个embedding。原先的参数量从 $O(n^2)$ 降低到了 $O(k \times n)$ 。ALBERT论文的因式分解思想跟这个非常相似：$O(V \times H) \ggg O(V \times E + E \times H)$

有了 $V$ 矩阵，上式就可以改写成如下形式：

$\hat{y}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n-1} \sum_{j=1}^{n} v_{i}^{T} v_{j} x_{i} x_{j}$

当 $k$ 足够大的时候，即 $k = n$ ，那么就有 $W = V$ 。在实际的应用场景当中，我们并不需要设置非常大的K，因为特征矩阵往往非常稀疏，我们可能没有足够多的样本来训练这么大量的参数，并且限制K也可以一定程度上提升FM模型的泛化能力。

此外这样做还有一个好处就是有利于模型训练，因为对于有些稀疏的特征组合来说，我们所有的样本当中可能都是空的。比如在刚才的例子当中用户A和电影B的组合，可能用户A在电影B上就没有过任何行为，那么这个数据就是空的，我们也不可能训练出任何参数来。但是引入了 $V$ 之后，虽然这两项缺失，但是我们针对用户A和电影B分别训练出了向量参数，我们用这两个向量参数点乘，就得到了这个交叉特征的系数。

虽然我们将模型的参数降低到了 $O(k \times n)$ ，但预测一条样本所需要的时间复杂度仍为 $O(k \times n^2)$ ，这仍然是不可接受的。所以对它进行优化也是必须的，并且这里的优化非常简单，可以直接通过数学公式的变形推导得到：

$\begin{aligned} \sum_{i=1}^{n} \sum_{j=i+1}^{n} v_{i}^{T} v_{j} x_{i} x_{j} &=\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} v_{i}^{T} v_{j} x_{i} x_{j}-\frac{1}{2} \sum_{i=1}^{n} v_{i}^{T} v_{j} x_{i} x_{j} \\ &=\frac{1}{2}\left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{j, f} x_{i} x_{j}-\sum_{i=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{i, f} x_{i} x_{i}\right) \\ &=\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)\left(\sum_{j=1}^{n} v_{j, f} x_{j}\right)-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \\ &=\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \end{aligned}$

FM模型预测的时间复杂度优化到了 $O(k \times n)$ .

模型训练

优化过后的式子如下：

$\hat{y}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right)$

针对FM模型我们一样可以使用梯度下降算法来进行优化。既然要使用梯度下降，那么我们就需要写出模型当中所有参数的偏导，主要分为三个部分：

$w_0$ : $\frac{\partial \theta}{\partial w_{0}}=1$
$\sum_{i=1}^{n} w_{i} x_{i}$ : $\frac{\partial 0}{\partial w_{i}}=x_{i}$
$\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right)$ : $\frac{\partial \hat{y}}{\partial v_{i, f}} = \frac{1}{2} (2x_i (\sum_{j=1}^{n} v_{j, f} x_{j}) - 2v_{i,f} x_i^2) = x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2}$

综合如下：

$\frac{\partial \hat{y}}{\partial \theta}= \begin{cases}1, & \text { if } \theta \text { is } w_{0} \\ x_{i}, & \text { if } \theta \text { is } w_{i} \\ x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2} & \text { if } \theta \text { is } v_{i, f}\end{cases}$

由于 $\sum_{j=1}^n v_{j,f} x_j$ 是可以提前计算好存储起来的，因此我们对所有参数的梯度计算也都能在 $O(1)$ 时间复杂度内完成。

拓展到 $d$ 维

参照刚才的公式，可以写出FM模型推广到d维的方程：

$\hat{y}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{l=2}^{d} \sum_{i_1=1}^{n-l+1} \cdots \sum_{i_{l}=i_{l-1}+1}^{n}\left(\Pi_{j-1}^{l} x_{i_{j}}\right)\left(\sum_{f=1}^{k} \Pi_{j=1}^{l} v_{i_{j}, f}^{l}\right)$

以 $d=3$ 为例，上式为：

$\hat{y}=w_{0}+\sum_{i=1}^{n} w_{i} x_{i} + \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} x_{i} x_{j}\left(\sum_{t=1}^{k} v_{i, t} v_{j, t}\right)+\sum_{i=1}^{n-2} \sum_{j=i+1}^{n-1} \sum_{l=j+1}^{n} x_{i} x_{j} x_{l}\left(\sum_{t=1}^{k} v_{i, t} v_{j, t} v_{l, t}\right)$

它的复杂度是 $O(k \times n^d)$ 。当 $d=2$ 的时候，我们通过一系列变形将它的复杂度优化到了 $O(k \times n)$ 。而当 $d > 2$ 的时候，没有很好的优化方法，而且三重特征的交叉往往没有意义，并且会过于稀疏，所以我们一般情况下只会使用 $d=2$ 的情况。

最佳实践

import torch
from torch import nn

ndim = len(feature_names)  # 原始特征数量
k = 4

class FM(nn.Module):
    def __init__(self, dim, k):
        super(FM, self).__init__()
        self.dim = dim
        self.k = k
        self.w = nn.Linear(self.dim, 1, bias=True)
        # 初始化V矩阵
        self.v = nn.Parameter(torch.rand(self.dim, self.k) / 100)
        
    def forward(self, x):
        linear = self.w(x)
        # 二次项
        quadradic = 0.5 * torch.sum(torch.pow(torch.mm(x, self.v), 2) - torch.mm(torch.pow(x, 2), torch.pow(self.v, 2)))
        # 套一层sigmoid转成分类模型，也可以不加，就是回归模型
        return torch.sigmoid(linear + quadradic)
    
    
fm = FM(ndim, k)
loss_fn = nn.BCELoss()
optimizer = torch.optim.SGD(fm.parameters(), lr=0.005, weight_decay=0.001)
iteration = 0
epochs = 10

for epoch in range(epochs):
    fm.train()
    for X, y in data_iter:
        output = fm(X)
        l = loss_fn(output.squeeze(dim=1), y)
        optimizer.zero_grad()
        l.backward()
        optimizer.step()
        iteration += 1        
        if iteration % 200 == 199:
            with torch.no_grad():
                fm.eval()
                output = fm(X_eva_tensor)
                l = loss_fn(output.squeeze(dim=1), y_eva_tensor)
                acc = ((torch.round(output).long() == y_eva_tensor.view(-1, 1).long()).sum().float().item()) / 1024
                print('Epoch: {}, iteration: {}, loss: {}, acc: {}'.format(epoch, iteration, l.item(), acc))
            fm.train()

DeepFM

$\hat{y}=\operatorname{sigmoid}\left(y_{F M}+y_{D N N}\right)$

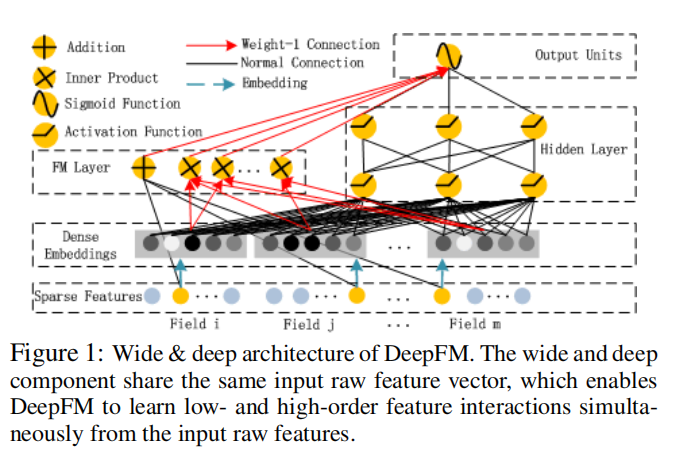
FM

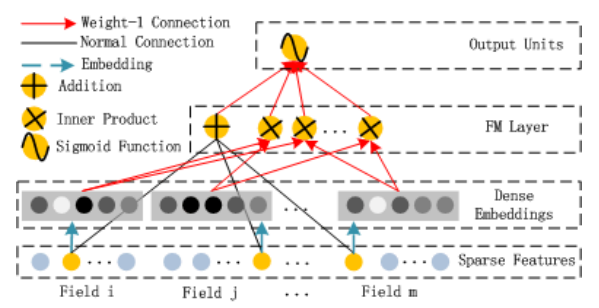
该组件就是在计算FM：

$y_{F M}=\langle w, x\rangle+\sum_{j_{1}=1}^{d} \sum_{j_{2}=j_{1}+1}^{d}\left\langle V_{i}, V_{j}\right\rangle x_{j_{1}} \cdot x_{j_{2}}$

注意不是：$w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right)$

每个 $Field$ 是one-hot形式，黄色的圆表示 $1$ ，蓝色的代表 $0$
连接黄色圆的黑线就是在做：$\langle w, x\rangle$
连接embedding的红色线就是在做：$\sum_{j_{1}=1}^{d} \sum_{j_{2}=j_{1}+1}^{d}\left\langle V_{i}, V_{j}\right\rangle x_{j_{1}} \cdot x_{j_{2}}$

DNN

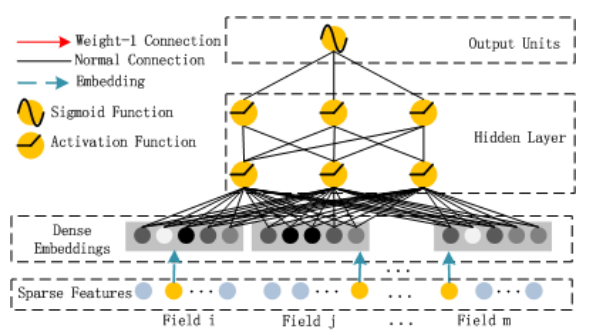
DNN部分比较简单，但它是与FM部分共享Embedding的。

FM

参数数量和时间复杂度优化

模型训练

拓展到 $d$ 维

最佳实践

DeepFM

FM

DNN

参考