VAE

这段时间看了VAE的有关知识，但网上关于VAE的讲解较为理论复杂，我这里就记录一下自己的想法了。

定义

VAE从概率的角度描述隐空间与输入样本，它将样本的隐变量建模为概率分布, 而非像AE一样把隐变量看做是离散的值。

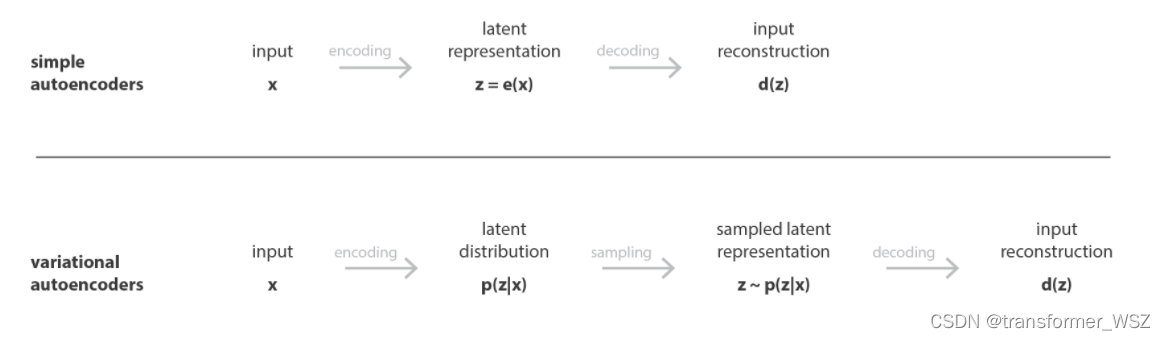
AE VS VAE

损失函数

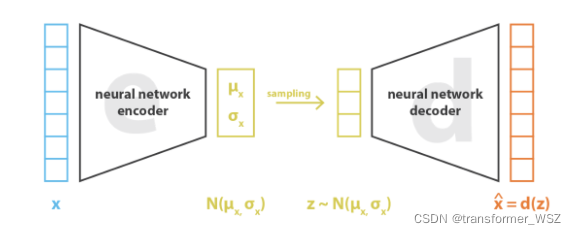
我们假设隐变量的概率分布为标准正态分布$N(0, 1)$（这种分布不是必须的，也可以是其它分布）。而描述正态分布需要有两个参数$\mu_x, \sigma_x$，在encoder端使用神经网络来拟合这两个参数。在decoder端，使用神经网络来还原出原始图像。因此，VAE的损失函数分为两部分：

• 正则化项，也就是KL Loss

• 重构损失

$$\begin{aligned} L &= L_{Recon} + L_{KL} \\ &= \|x-\hat{x}\|^{2}+\mathrm{KL}[N(\mu_{x}, \sigma_{x}), N(0, 1)] \\ &= \|x-d(z)\|^{2}+KL[N(\mu_{x}, \sigma_{x}), N(0, 1)] \end{aligned}$$

关于$KL\left[N\left(\mu_{x}, \sigma_{x}\right), N(0,1)\right]$的推导如下：

$$\begin{aligned} & KL\left(N\left(\mu, \sigma^{2}\right) \| N(0,1)\right) \\ &= \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} }\left(\log \frac{\frac{e^{ \frac{-(x-\mu)^{2}}{2 \sigma^{2}} }}{\sqrt{2 \pi \sigma^{2}}} }{\frac{e^{\frac{-x^{2}}{2}}}{\sqrt{2 \pi}} }\right) d x \\ &= \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} } \log \left\{\frac{1}{\sqrt{\sigma^{2}}} \exp \left\{\frac{1}{2}\left[x^{2}- \frac{(x-\mu)^{2}}{\sigma^{2}} \right]\right\}\right\} d x \\ &= \frac{1}{2} \int \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}} }\left[-\log \sigma^{2}+x^{2}- \frac{(x-\mu)^{2}}{\sigma^{2}} \right] d x \\ &= \frac{1}{2}\left(-\log \sigma^{2}+\mu^{2}+\sigma^{2}-1\right) \end{aligned}$$

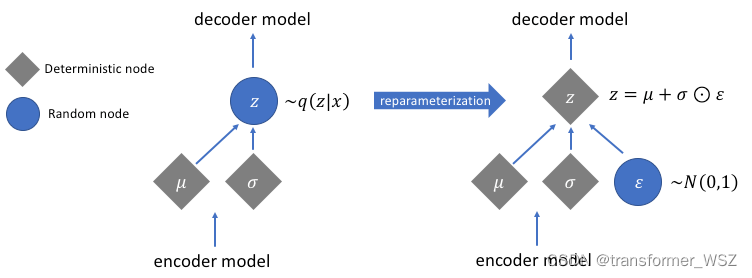
重参数技巧

我们从概率分布中采样出 $z$ ，但是该过程是不可导的。VAE通过重参数化使得梯度不因采样而断裂。

总结

其实VAE可以看成一个做降维的model，我们希望把一个高维的特征投影到一个低维的流型上。而在VAE中，这个低维流型就是一个多元标准正态分布。为了使投影准确，于是通过希望每一个样本$X_i$的计算出来的期望与方差都接近与我们希望投影的分布，所以这里就有了KL Loss。至于重构损失，是可以使采样的时候更加准确，能够采样到我们在encode的时候投影到的点。

最佳实践

• Pytorch实现: VAE 这篇博客实现了VAE，整体上代码简单易懂。在generation阶段，我们只需从学习到的概率分布中采样，然后送入decoder中解码，即可获得生成的图片。

• 小小将的VAE实现，可以直接运行：https://github.com/xiaohu2015/nngen/blob/main/models/vae.ipynb

---

参考

• 变分自编码器VAE：原来是这么一回事

• Understanding Variational Autoencoders (VAEs)

• Pytorch实现: VAE

• 变分自编码器入门

• VAE.ipynb - Colaboratory

• 李宏毅2021春机器学习课程

• VAE.pdf(ntu.edu.tw))

• VAE的推导