
无监督学习中的典型代表,它将类别相同的样本汇聚在一起,但是聚类好之后,它并不知道每个样本的类别(看到之前有些博客说做分类的,当时一直困扰我,现在才知道这只是聚类,不是分类)。
算法流程
- 随机选择 $k$ 个样本作为初始化聚类中心:$a_1, a_2, \dots, a_k$ ;
- 针对数据集每个样本 $x_i$ ,计算其到每个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中;
- 针对每个类别 $a_j$ ,重新计算它的聚类中心:$a_j = \frac{1}{|c_j|} \sum_{x \in c_j} x$ (即该类所有样本的质心);
- 重复2-3步,直到达到某个终止条件(迭代次数、最小误差变化等)。
优缺点
优点
- 容易理解,聚类效果不错,虽然是局部最优, 往往局部最优已经足够
- 处理大数据集的时候,该算法可以保证较好的伸缩性
- 算法复杂性低
缺点
- $K$ 需要认为设定,不同的取值对最终聚类效果影响非常大
- 对初始簇类中心敏感,不同的初始取值对最终聚类效果影响非常大
- 对异常值敏感
- 不适合离散的分类、样本类别不平衡的分类、非凸形状的分类
如何选择 $K$ 值?
基本思想还是最小化类内距离,最大化类间距离,使同一簇内样本尽可能相似,不同簇中样本尽可能不相似。
手肘法
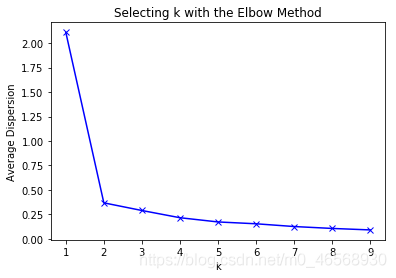
随着 $K$ 值增大,误差值会越来越小(举一个极端的例子:当每一个样本被分为一个类时,类内间距最小,但这显然不是我们想要的)。因此可根据不同 $K$ 值下的误差曲线选择使误差平方和下降最快的 $K$ 值。当大于此 $K$ 值时,$K$ 值增大,但误差减少量很小。即选择曲线上的拐点最佳。在下面这个图中即选择 $k=2$ ,将样本分为两类。
Gap statistic
手肘法的缺点在于需要人工看不够自动化,这里提出Gap statistic:
其中 $D_k$ 为损失函数,这里 $E(log D_k)$ 指的是 $log(D_k)$ 的期望。这个数值通常通过蒙特卡洛模拟产生,我们在样本里所在的区域中按照均匀分布随机产生和原始样本数一样多的随机样本,并对这个随机样本做 K-Means,从而得到一个 $D_k$ 。如此往复多次,通常20次,我们可以得到20个 $log D_k$ 。对这20个数值求平均值,就得到了 $E(log D_k)$ 的近似值。最终可以计算 Gap Statisitc。而 Gap statistic 取得最大值所对应的 $K$ 就是最佳的 $K$ 。
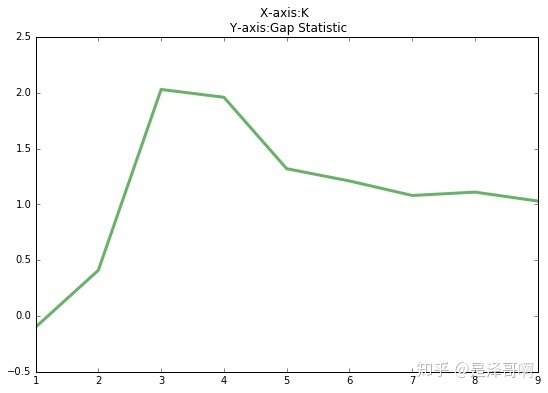
由图可见,当 $K=3$ 时,$Gap(K)$ 取值最大,所以最佳的簇数是 $K=3$ 。
如何初始化聚类中心?
这里主要介绍K-means++算法,主要思想是选择离已选中心点最远的点。这也比较符合常理,聚类中心当然是互相离得越远越好。
算法流程如下:
随机选择一个中心点 $a_1$ ;
对于数据集中的每一个点 $x_i$ ,计算它与之前 $n$ 个聚类中心最远的距离 $D(x_i)$ ,并以 $\frac{D(x_i)^2}{\sum_{j=1}^n D(x_j)^2}$ 的概率选择作为新中心点 $a_i$ ;
重复2步骤,直到选出 $K$ 个聚类中心。