AdaBoost

AdaBoost 是属于 boosting 的一种经典算法。

Overview

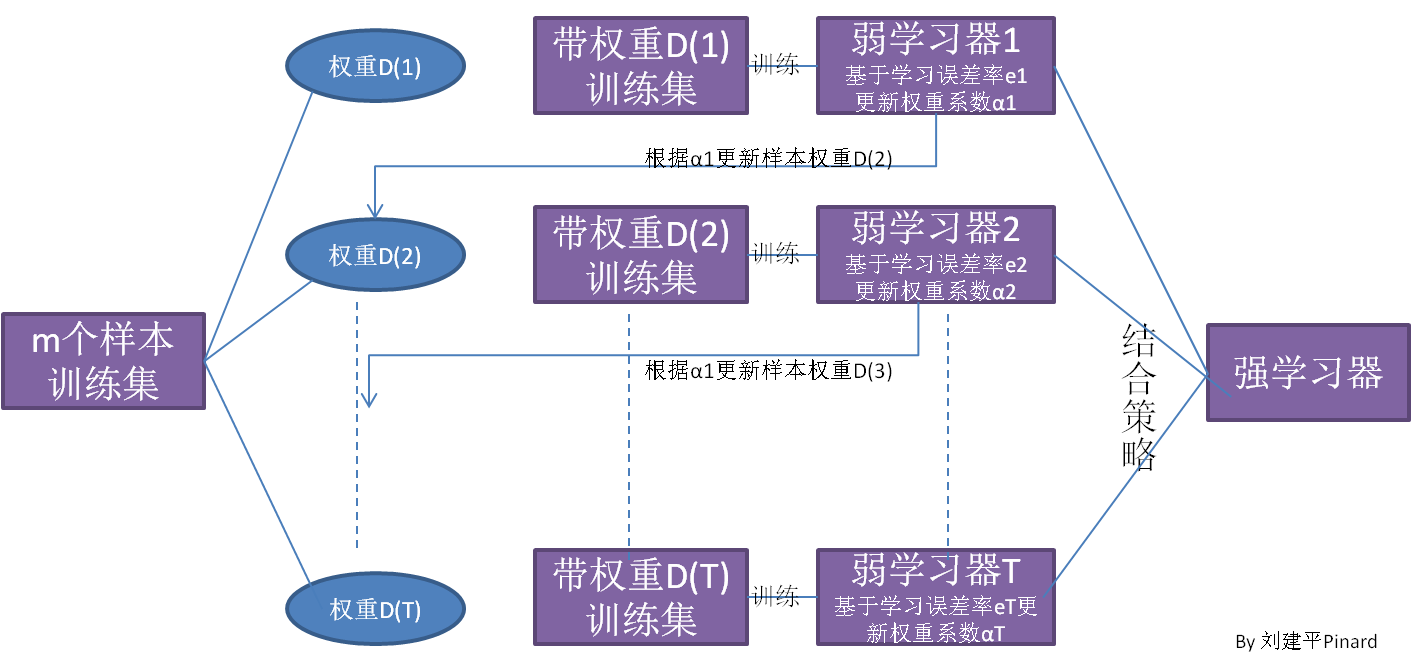
AdaBoost算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2。如此重复进行，直到弱学习器数达到事先指定的数目 $T$ ，最终将这 $T$ 个弱学习器通过集合策略进行整合，得到最终的强学习器。

AdaBoost分类算法流程

输入样本集 $\boldsymbol{T}=\left\{\left(x, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots\left(x_{m}, y_{m}\right)\right\}$ ，类别为$\{ -1, +1 \}$，弱分类器迭代次数 $K$。输出为最终的强分类器 $f(x)$ 。

1. 初始化样本集权重为：

   $$D(1)=\left(w_{11}, w_{12}, \ldots w_{1 m}\right) ; \quad w_{1 i}=\frac{1}{m} ; \quad i=1,2 \ldots m$$

2. 对于 $k=1, 2, \dots, K$ ：

   1. 使用具有权重 $D_k$ 的样本集来训练数据，得到弱分类器 $G_k(x)$

   2. 计算 $G_k(x)$ 的分类误差率：

      $$e_{k}=P\left(G_{k}\left(x_{i}\right) \neq y_{i}\right)=\sum_{i=1}^{m} w_{k i} I\left(G_{k}\left(x_{i}\right) \neq y_{i}\right)$$

   3. 计算弱分类器的权重系数：

      $$\alpha_{k}=\frac{1}{2} \log \frac{1-e_{k}}{e_{k}}$$

      从上式可以看出，如果分类误差率 $e_k$ 越大，则对应的弱分类器权重系数 $\alpha_{k}$ 越小。即误差率小的弱分类器权重系数越大。

   4. 更新样本集的权重分布：

      $$w_{k+1, i}=\frac{w_{k i}}{Z_{K}} \exp \left(-\alpha_{k} y_{i} G_{k}\left(x_{i}\right)\right) \quad i=1,2, \ldots m$$

      其中 $Z_K$ 是归一化因子：

      $$Z_{k}=\sum_{i=1}^{m} w_{k i} \exp \left(-\alpha_{k} y_{i} G_{k}\left(x_{i}\right)\right)$$

      从上式可以看出，如果第 $i$ 个样本分类错误，则 $y_{i} G_{k} < 0$ ，导致样本的权重在第 $k+1$ 个弱分类器中增大；如果分类正确，则权重在第 $k+1$ 个弱分类器中减少。

3. 构建最终分类器：

   $$f(x)=\operatorname{sign}\left(\sum_{k=1}^{K} \alpha_{k} G_{k}(x)\right)$$

对于Adaboost多元分类算法，其原理和二元分类类似。最主要区别在弱分类器的系数上。比如Adaboost SAMME算法，它的弱分类器的系数：

$$\alpha_{k}=\frac{1}{2} \log \frac{1-e_{k}}{e_{k}}+\log (R-1)$$

其中 $R$ 为类别数。如果 $R=2$ ，那么上式即是二分类的弱分类器系数。

AdaBoost回归算法流程

输入样本集 $\boldsymbol{T}=\left\{\left(x, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots\left(x_{m}, y_{m}\right)\right\}$ ，弱分类器迭代次数 $K$。输出为最终的强分类器 $f(x)$ 。

1. 初始化样本集权重为：

   $$D(1)=\left(w_{11}, w_{12}, \ldots w_{1 m}\right) ; \quad w_{1 i}=\frac{1}{m} ; \quad i=1,2 \ldots m$$

2. 对于 $k=1, 2, \dots, K$ ：

   1. 使用具有权重 $D_k$ 的样本集来训练数据，得到弱分类器 $G_k(x)$

   2. 计算训练集上的最大误差：

      $$E_{k}=\max \left|y_{i}-G_{k}\left(x_{i}\right)\right| i=1,2 \ldots m$$

   3. 计算每个样本的相对误差：

      • 线性误差：$e_{k i}=\frac{\left|y_{i}-G_{k}\left(x_{i}\right)\right|}{E_{k}}$
      • 平方误差：$e_{k i}=\frac{(y_{i}-G_{k}(x_{i}))^2}{E_{k}^2}$
      • 指数误差：$e_{k i}=1-\exp \left(\frac{-\left|y_{i}-G_{k}\left(x_{i}\right)\right|}{E_{k}}\right)$

   4. 计算回归误差率：

      $$e_k = \sum_{i=1}^m w_{ki} e_{ki}$$

   5. 计算弱学习器的权重系数：

      $$a_k = \frac{1-e_k}{e_k}$$

   6. 更新样本集的权重分布：

      $$w_{k+1, i}=\frac{w_{k i}}{Z_{k}} \alpha_{k}^{1-e_{k i}}$$

      其中 $Z_K$ 是归一化因子：

      $$Z_{k}=\sum_{i=1}^{m} w_{k i} \alpha_{k}^{1-e_{k i}}$$

3. 构建最终强学习器：

   $$f(x)=G_{k^{*}}(x)$$

即取所有 $ ln \frac{1}{\alpha_{k}}, k=1,2, \ldots . K$ 的中位数值对于序号 $k^{*}$ 对应的弱学习器。

AdaBoost正则化

为了防止AdaBoost过拟合，我们加入正则化项：

$$f_{k}(x)=f_{k-1}(x)+v \alpha_{k} G_{k}(x), \quad 0 < v <= 1$$

与GBDT类似，该正则化项称作学习率。对于同样的训练集学习效果，较小的 $v$ 意味着我们需要更多的弱学习器的迭代次数。

AdaBoost总结

优点

• Adaboost作为分类器时，分类精度很高
• 在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活
• 不容易发生过拟合

缺点

• 对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性

---

参考

• Adaboost入门教程——最通俗易懂的原理介绍（图文实例）
• 集成学习之Adaboost算法原理小结