记录一下XGBoost的的学习过程。
示例
我们要预测一家人对电子游戏的喜好程度,有年龄、性别、职业这些特征。根据之前训练出来的多棵树来对这些样本打分,如下图所示:
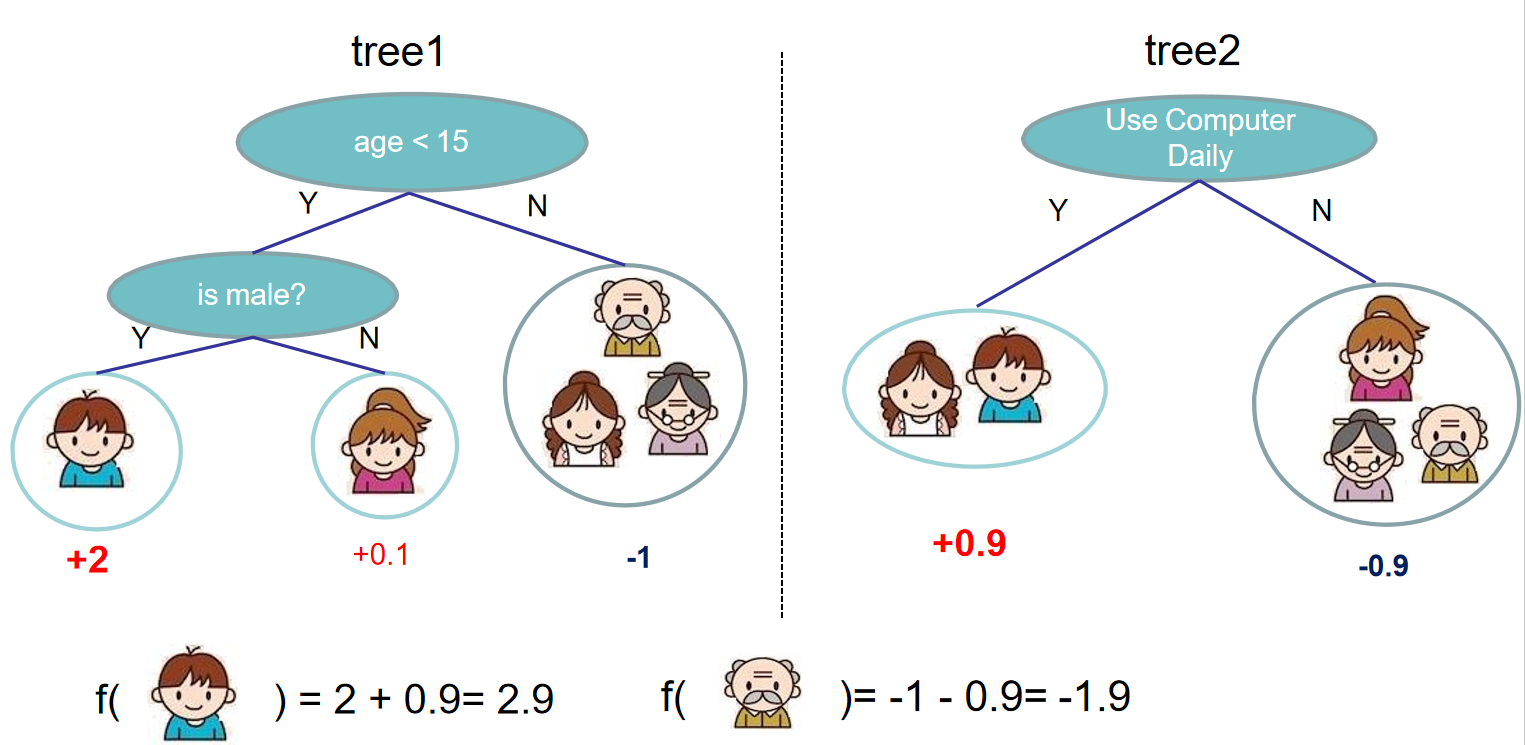
注意,上述分数是由训练所得。与GBDT类似,两棵树的结论累加起来便是最终结论。如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义:
前 $t-1$ 棵树的复杂度之和可以用一个常量 $constant$ 表示。上述公式由两部分组成:
- 损失函数:揭示训练误差
- 正则化项:惩罚复杂模型
推导
损失函数
前沿知识:泰勒展开式:
定义如下符号:
因此:
对应关系如下:
- (1)式 $x$ $\Leftrightarrow$ (2)式 $\hat{y_i}^{(t-1)}$
- (1)式 $\Delta x$ $\Leftrightarrow$ (2)式 $f_{t}\left(x_{i}\right)$
由于 $\hat{y_i}^{(t-1)}$ 是已知的,因此 $l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)$ 也是个常数项,可以合并到 $constant$ 去。将 $constant$ 去掉,上述公式可以简化为:
正则化项
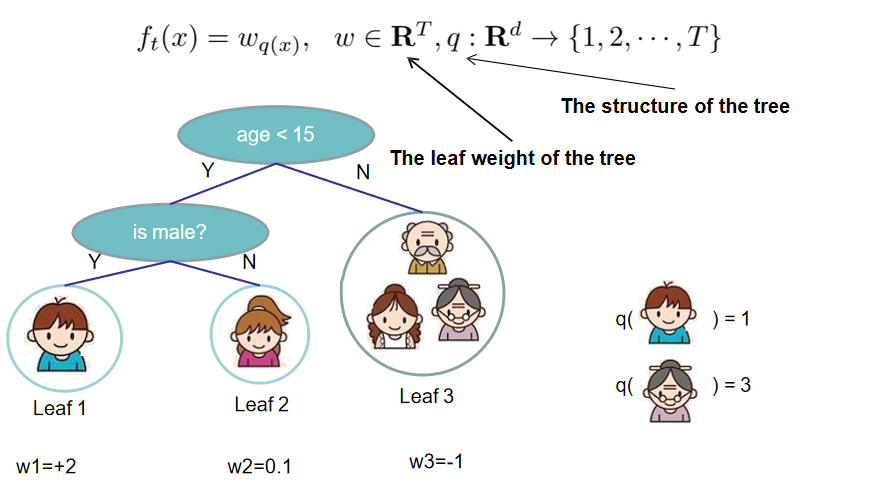
- $q(x)$ 表示将样本 $x$ 映射到某个叶子节点的编号上
- $w$ 表示叶子节点的得分
注意,多个样本可以落到同一个叶子节点上,这时它们的得分是一样的。
XGBoost定义树的复杂度如下:
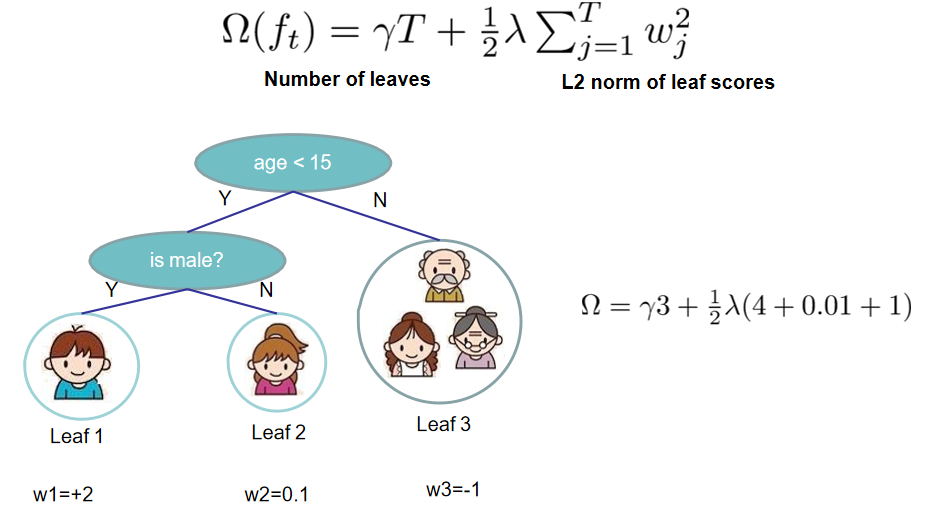
重新组织损失函数
由于 $w$ 是我们要求的参数,因此将上述公式组织成关于 $w$ 的函数:
- $I_{j}=\left\{i \mid q\left(x_{i}\right)=j\right\}$ 表示样本下标集合:这些样本可以落到下标为 $j$ 的叶子节点
这样上式可以看作关于 $w$ 的一元二次函数。
定义 $G_{j}=\sum_{i \in I_{j}} g_{i} \quad H_{j}=\sum_{i \in I_{j}} h_{i}$ ,上式继续简化为:
当 $w_j = - \frac{G_j}{H_j + \lambda}$ 时,$Obj^{(t)}$ 取得最小:$-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T$
下图给个示例:

FAQ
1. 二阶泰勒展开的优势在哪儿?
PPT上是这样说的:

主要有如下两点理由:
- XGBoost是以mse为基础推导出来的,在mse的情况下,xgboost的目标函数展开就是一阶项+二阶项的形式,而其他类似logloss这样的目标函数不能表示成这种形式。为了后续推导的统一,所以将目标函数进行二阶泰勒展开,就可以直接自定义损失函数了,只要二阶可导即可,增强了模型的扩展性。
- 二阶信息能够让梯度收敛的更快,类似牛顿法比SGD收敛更快。一阶信息描述梯度变化方向,二阶信息可以描述梯度变化方向是如何变化的。
2. XGBoost与GBDT的区别
- 基分类器:XGBoost的基分类器不仅支持CART决策树,还支持线性分类器,此时XGBoost相当于带L1和L2正则化项的逻辑回归或者线性回归。
- 导数信息:XGBoost对损失函数做了二阶泰勒展开,GBDT只用了一阶导数信息,并且XGBoost还支持自定义损失函数,只要损失函数一阶、二阶可导。
- 正则项:XGBoost的目标函数加了正则项, 相当于预剪枝,使得学习出来的模型更加不容易过拟合。
- 列抽样:XGBoost支持列采样,与随机森林类似,用于防止过拟合。
- 缺失值处理:对树中的每个非叶子结点,XGBoost可以自动学习出它的默认分裂方向。如果某个样本该特征值缺失,会将其划入默认分支。
- 并行化:注意不是tree维度的并行,而是特征维度的并行。XGBoost预先将每个特征按特征值排好序,存储为块结构,分裂结点时可以采用多线程并行查找每个特征的最佳分割点,极大提升训练速度。
3. XGBoost为什么可以并行训练?
- XGBoost的并行,并不是说每棵树可以并行训练,XGB本质上仍然采用boosting思想,每棵树训练前需要等前面的树训练完成才能开始训练。
- XGBoost的并行,指的是特征维度的并行:在训练之前,每个特征按特征值对样本进行预排序,并存储为Block结构,在后面查找特征分割点时可以重复使用,而且特征已经被存储为一个个block结构,那么在寻找每个特征的最佳分割点时,可以利用多线程对每个block并行计算。
4. XGBoost如何防止过拟合?
- 目标函数添加正则项:叶子节点个数+叶子节点权重的L2正则化
- 列抽样:训练的时候只用一部分特征(不考虑剩余的block块即可)
- 子采样:每轮计算可以不使用全部样本,使算法更加保守
- shrinkage: 可以叫学习率或步长,为了给后面的训练留出更多的学习空间
5. XGBoost如何处理缺失值?
- 在特征 $k$ 上寻找最佳分割点时,不会对该列特征缺失的样本进行遍历,而只对该列特征值为非缺失的样本上对应的特征值进行遍历,通过这个技巧来减少了为稀疏离散特征寻找分割点的时间开销。
- 在逻辑实现上,为了保证完备性,会将该特征值缺失的样本分别分配到左叶子结点和右叶子结点,两种情形都计算一遍后,选择分裂后增益最大的那个方向(左分支或是右分支),作为预测时特征值缺失样本的默认分支方向。
- 如果在训练中没有缺失值而在预测中出现缺失,那么会自动将缺失值的划分方向放到右子结点。
6. XGBoost中的一棵树的停止生长条件
- 当新引入的一次分裂所带来的增益 $Gain < \gamma$ 时,放弃当前的分裂。
- 当树达到最大深度时,停止建树,因为树的深度太深容易出现过拟合。
- 当引入一次分裂后,重新计算新生成的左、右两个叶子结点的样本权重和。如果任一个叶子结点的样本权重低于某一个阈值,也会放弃此次分裂。如果一个叶子节点包含的样本数量太少也会放弃分裂,防止树分的太细。
7. XGBoost中如何对树进行剪枝?
- 在目标函数中增加了正则项:使用叶子结点的数目和叶子结点权重的L2模的平方,控制树的复杂度。
- 在结点分裂时,定义了一个阈值,如果分裂后目标函数的增益小于该阈值,则不分裂。
- 当引入一次分裂后,重新计算新生成的左、右两个叶子结点的样本权重和。如果任一个叶子结点的样本权重低于某一个阈值(最小样本权重和),也会放弃此次分裂。
- XGBoost 先从顶到底建立树直到最大深度,再从底到顶反向检查是否有不满足分裂条件的结点,进行剪枝。
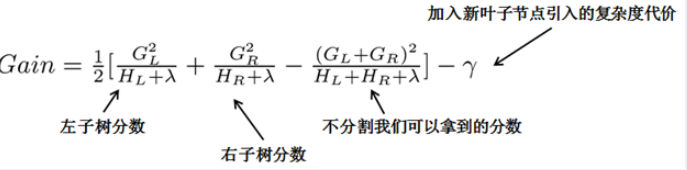
8. XGBoost如何分裂节点?
从树深度0开始,每一节点都遍历所有的特征,比如年龄、性别等等,然后对于某个特征,先按照该特征里的值进行排序,然后线性扫描该特征进而确定最好的分割点,最后对所有特征进行分割后,我们选择所谓的增益Gain最高的那个特征。Gain的计算公式如下: