GCN

最近两周断断续续学习了GCN有关的知识，在此主要记录一下GCN状态更新的公式推导。

图卷积起缘

我们先探讨一个问题：为什么研究者们要设计图卷积操作，传统的卷积不能直接用在图上吗？ 要理解这个问题，我们首先要理解能够应用传统卷积的图像(欧式空间)与图(非欧空间)的区别。如果把图像中的每个像素点视作一个结点，如下图左侧所示，一张图片就可以看作一个非常稠密的图；下图右侧则是一个普通的图。阴影部分代表卷积核，左侧是一个传统的卷积核，右侧则是一个图卷积核。

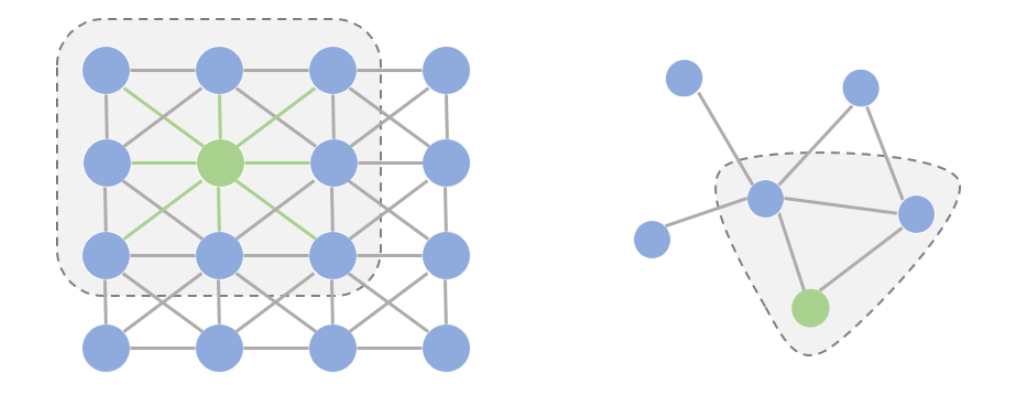
仔细观察上图，可以发现两点不同：

1. 在图像为代表的欧式空间中，结点的邻居数量都是固定的。比如说绿色结点的邻居始终是8个(边缘上的点可以做Padding填充)。但在图这种非欧空间中，结点有多少邻居并不固定。目前绿色结点的邻居结点有2个，但其他结点也会有5个邻居的情况。

2. 欧式空间中的卷积操作实际上是用固定大小可学习的卷积核来抽取像素的特征，比如这里就是抽取绿色结点对应像素及其相邻像素点的特征。但是因为图里的邻居结点不固定，所以传统的卷积核不能直接用于抽取图上结点的特征。

真正的难点聚焦于邻居结点数量不固定上。目前主流的研究从2条路来解决这件事：

1. 提出一种方式把非欧空间的图转换成欧式空间。

2. 找出一种可处理变长邻居结点的卷积核在图上抽取特征。

这两条实际上也是后续图卷积神经网络的设计原则，图卷积的本质是想找到适用于图的可学习卷积核。

图卷积框架

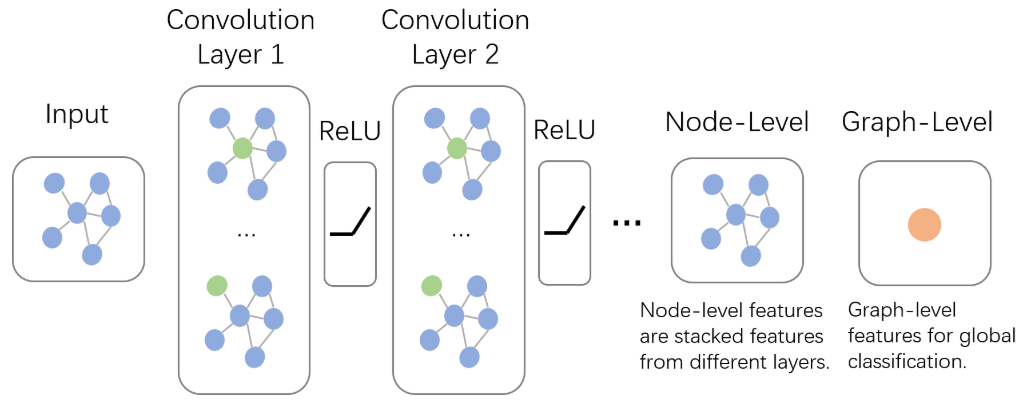
如上图所示，输入的是整张图，前向传播过程如下：

1. 在Convolution Layer 1里，对每个结点的邻居都进行一次卷积操作，并用卷积的结果更新该结点；

2. 经过激活函数如ReLU；

3. 再过一层卷积层Convolution Layer 2与一层激活函数；

4. 重复1~3步骤，直到层数达到预期深度。

与GNN类似，图卷积神经网络也有一个局部输出函数，用于将结点的状态(包括隐藏状态与结点特征)转换成任务相关的标签，比如水军账号分类，这种任务称为Node-Level的任务；也有一些任务是对整张图进行分类的，比如化合物分类，这种任务称为Graph-Level的任务。卷积操作关心每个结点的隐藏状态如何更新，而对于Graph-Level的任务，它们会在卷积层后加入更多操作。

卷积操作

空域卷积(Spatial Convolution)

从设计理念上看，空域卷积与深度学习中的卷积的应用方式类似，其核心在于聚合邻居结点的信息。比如说，一种最简单的无参卷积方式可以是：将所有直连邻居结点的隐藏状态加和，来更新当前结点的隐藏状态。

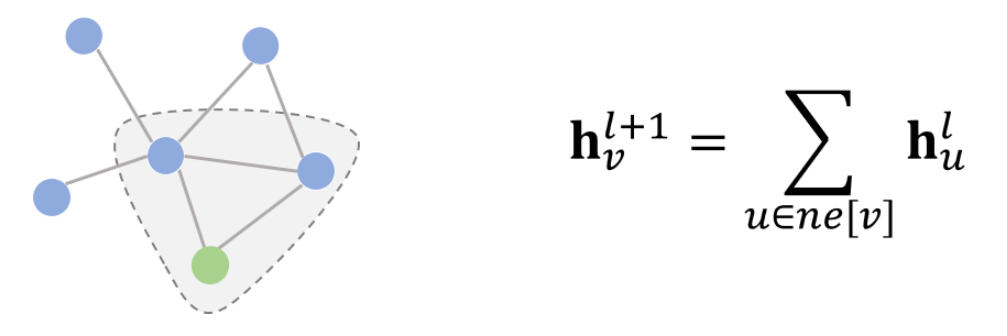
常见的空域卷积网络有如下几种：

• 消息传递网络(Message Passing Neural Network)

• 图采样与聚合(Graph Sample and Aggregate)

• 图结构序列化(PATCHY-SAN)

频域卷积(Spectral Convolution)

空域卷积非常直观地借鉴了图像里的卷积操作，但它缺乏一定的理论基础。而频域卷积则不同，它主要利用的是图傅里叶变换(Graph Fourier Transform)实现卷积。简单来讲，它利用图的拉普拉斯矩阵(Laplacian matrix)导出其频域上的的拉普拉斯算子，再类比频域上的欧式空间中的卷积，导出图卷积的公式。虽然公式的形式与空域卷积非常相似，但频域卷积的推导过程却有些艰深晦涩。因此本文主要来推导GCN的状态更新公式。

傅里叶变换(Fourier Transform)

FT会将一个在空域(或时域)上定义的函数分解成频域上的若干频率成分。换句话说，傅里叶变换可以将一个函数从空域变到频域。用 $F$ 来表示傅里叶变换的话，这里有一个很重要的恒等式：

$$(f * g)(t) = F^{-1}[F[f(t)] \odot F[g(t)]]$$

$f$ 经过傅里叶变换后 $\hat{f}$ 如下所示：

$$\hat{f}(t)=\int f(x) e^{-2 \pi i x t} d x$$

其中$i = \sqrt{-1}$ 是虚数单位，$t$ 是任意实数。$e^{-2 \pi i x t}$ 是类比构造傅里叶变换的关键。它实际上是拉普拉斯算子$\Delta$的广义特征函数。

特征向量需要满足的定义式是：对于矩阵$A$，其特征向量满足的条件应是矩阵与特征向量$x$做乘法的结果，与特征向量乘标量λλ的结果一样，即满足如下等式：

$$Ax = \lambda x$$

$\Delta$ 作用在 $e^{-2 \pi i x t}$ 满足上述特征向量的定义：

$$\Delta e^{-2 \pi i x t}=\frac{\partial^{2}}{\partial t^{2}} e^{-2 \pi i x t}=-4 \pi^{2} x^{2} \exp ^{-2 \pi i x t}$$

$\Delta$ 即为 $-4 \pi^2 x^2$，注意这里 $t$ 是变量，$x$ 是常量。本质上，傅里叶变换是将$f(t)$映射到了以$\left\{e^{-2 \pi i x t}\right\}$为基向量的空间中。

图上的傅里叶变换

图上的拉普拉斯矩阵 $L$ 可以按照如下公式分解：

$$\begin{array}{c} L= I_N - D^{- \frac {1} {2}}AD^{- \frac {1} {2}} = U \Lambda U^{T} \\ U=\left(u_{1}, u_{2}, \cdots, u_{n}\right) \\ \Lambda=\left[\begin{array}{ccc} \lambda_{1} & \dots & 0 \\ \dots & \dots & \dots \\ 0 & \dots & \lambda_{n} \end{array}\right] \end{array}$$

$I_N$ 为单位矩阵，$D$ 为度矩阵，$A$ 为领阶矩阵，$u$ 是特征向量，$\lambda$ 是特征值。

图上的卷积与传统的卷积非常相似，这里 $f$ 是特征函数，$g$ 是卷积核：

$$\begin{array}{c} (f * g)=F^{-1}[F[f] \odot F[g]] \\ \left(f *_{G} g\right)=U\left(U^{T} f \odot U^{T} g\right)=U\left(U^{T} g \odot U^{T} f\right) \end{array}$$

如果把 $U^{T} g$ 整体看作可学习的卷积核，记作 $g_{\theta}$ ，最终图上的卷积公式即是：

$$o=\left(f *_{G} g\right)_{\theta}=U g_{\theta} U^{T} f$$

推导

频域卷积即是在 $g_\theta$ 上做文章。类比 $L$ 的分解公式，我们将 $g_\theta$ 看作是 $\Lambda$ 的函数 $g_\theta(\Lambda)$ 。由于特征分解计算量是非常巨大的，使用Chebyshev对 $g_\theta(\Lambda)$ 做近似估计：

$$g_{\theta^{\prime}}(\Lambda) \approx \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{\Lambda})$$

$\tilde{\Lambda}=\frac{2}{\lambda_{\max }} \Lambda-I_{N}$ ，$\theta^{\prime} \in \mathbb{R}^{K}$ 是Chebyshev系数。切比雪夫多项式是递归定义的：$T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x), T_0(x) = 1, T_1(x) = x$ 。

基于上述假设，图上卷积公式近似为：

$$o \approx \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{\Lambda}) f = \sum_{k=0}^{K} \theta_{k}^{\prime} T_{k}(\tilde{L}) f$$

$\tilde{L}=\frac{2}{\lambda_{max}} L-I_{N}$，因为$\left(U \Lambda U^{\top}\right)^{k}=U \Lambda^{k} U^{\top}$

取$K = 1$，将上述公式展开：

$$o \approx \theta_{0}^{\prime} f + \theta_{1}^{\prime}\left(L-I_{N}\right) f = \theta_{0}^{\prime} f - \theta_{1}^{\prime} D^{-\frac{1}{2}} A D^{-\frac{1}{2}} f$$

为了防止模型过拟合，我们还可以将参数进一步合并：

$$o \approx \theta\left(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) f$$

$\theta=\theta_{0}^{\prime}=-\theta_{1}^{\prime}$，$I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$ 的特征值取值范围现在是 $[0, 2]$ 。为了防止误差在反向传播的过程中出现梯度弥散，将该式进行归一化：

$$I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} \\ \tilde{A}=A+I_{N} \\ \tilde{D}_{i i}=\sum_{j} \tilde{A}_{i j}$$

现在我们可以将 $l$ 层隐藏状态 $H^l \in \mathbb{R}^{N \times C}$ ，$C$ 是某个node的特征数量，那么最终的状态更新公式为：

$$H^{l+1} = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^l \Theta$$

$\Theta \in \mathbb{R}^{C \times F}$ 是可训练的卷积核参数。

最佳实践

Graph Convolutional Networks for Text Classification 该篇论文使用GCN对圣经的章节进行分类。具体的实现思路见Text-based Graph Convolutional Network — Bible Book Classification，代码见 https://github.com/plkmo/Bible_Text_GCN

---

参考

• 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (二)
• 图卷积网络(GCN)新手村完全指南