
在看师兄的论文时,里面涉及到强化学习的 Policy Gradient 。看了网上好多博客,觉得公式推导太复杂了,断断续续地持续了三周。今天静下心来看了一遍,发现没有那么难,果然做学术还是不能浮躁啊!
前言
强化学习是机器学习的一个分支,但是它与我们常见监督式学习不太一样。从学习方式上讲强化学习更加接近人类的学习,例如当你接触一款新的电子游戏的时候,虽然看不懂屏幕的提示,但是经过自己的摸索也能掌握游戏方法,这个摸索的过程其实就是通过试错逐渐了解游戏规则的学习过程。同样,强化学习也是通过一系列的尝试并根据得到的反馈不断调整自己的行为来学习陌生的对象。
强化学习主要包括如下几个部分:
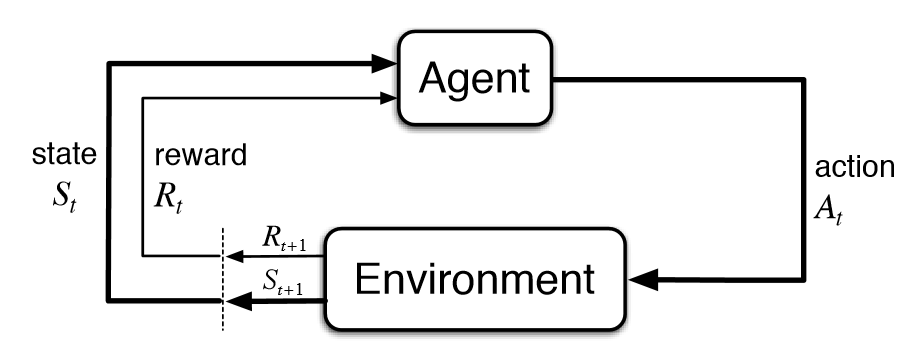
- 主体(Agent): 指能够通过动作与环境交互的对象,强化学习中主体通常是运行中的算法,比如在游戏中的主体是用于控制本方球拍的算法。
- 环境(Environment): 指主体动作作用的对象, 比如游戏本身。
- 动作(Action): 指所有可能作用于环境上的操作,比如游戏中算法控制球拍上下移动。
- 状态(State): 指可被主体感知的关于环境的信息,比如游戏中屏幕显示的球和球拍的位置以及移动方向和速度信息。
- 奖励(Reward): 指由环境回馈给主体的描述上一个动作效果的信息,比如游戏中球拍动作导致双方的得分变化。
强化学习的过程是一个通过和环境交互获得反馈,再根据反馈调整动作以期使总奖励最大化的过程,这个是一个多步 (multi timestep) 的交互的过程,每一步交互都会影响其后的所有步骤。强化学习中的一次交互是指主体对环境施加一个动作,环境的状态发生改变并且回馈给主体一个奖励(奖励既可以是正向的,如本方得分增加;也可以是负向的,如对方得分增加)。强化学习的目标就是寻找一个最优的策略使得整个学习过程(从开始状态到终结状态)获得的奖励最大化。
在实现上,强化学习是一个通过多个轮次逐渐优化算法的参数从而增强学习效果的过程,每个轮次包含两部分:前向反馈(feed forward)和反向传播(back propagation)。处于初始状态的主体根据算法的当前参数生成动作作用于环境,环境返回给主体新的状态和对动作的奖励,在轮次结束后算法通过汇总所有在本轮收集到的反馈调整算法的参数开始下一轮的学习,直到学习的效果不再增强。
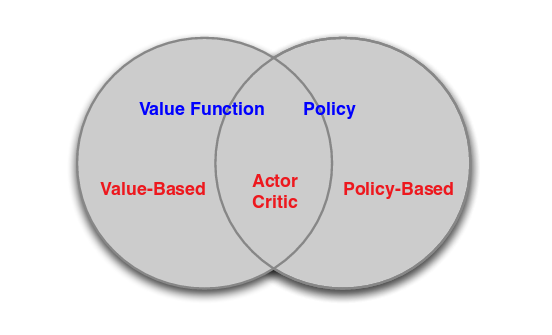
强化学习包括了一系列不同的算法(如下图),其中比较常见的是基于值(Value-based)的方法和基于策略(Policy-based)的方法。这两类方法各有特点,适用于解决不同的问题。一般来说,基于值的方法适用于比较简单(状态空间比较小)的问题,它有较高的数据利用率并且能稳定收敛;而基于策略的方法适用于复杂问题,但是高方差是这类方法会存在的一个比较明显的问题。
策略梯度
原理
基于值的方法一般是确定性的,给定一个状态就能计算出每种可能动作的奖励(确定值),但这种确定性的方法恰恰无法处理一些现实的问题,比如玩 100 把石头剪刀布的游戏,最好的解法是随机的使用石头、剪刀和布并尽量保证这三种手势出现的概率一样,因为任何一种手势的概率高于其他手势都会被对手注意到并使用相应的手势赢得游戏。
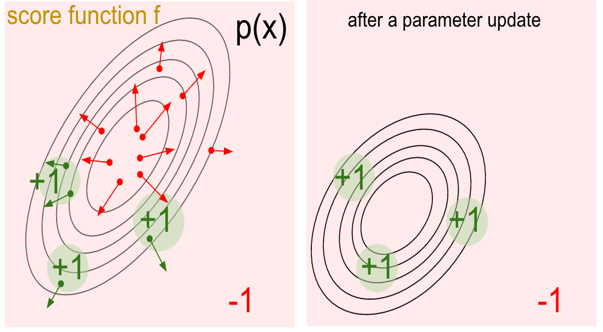
策略梯度正是为了解决上面的问题产生的,而它的秘密武器就是随机(Stochastic)。首先随机能提供非确定的结果,但这种非确定的结果并不是完全的随意而是服从某种概率分布的随机,策略梯度不计算奖励(reward)而是使用概率选择动作,这样就避免了因为计算奖励而维护状态表。策略梯度的基本原理是通过反馈调整策略,具体来说就是在得到正向奖励时,增加相应的动作的概率;得到负向的奖励时,降低相应动作的概率。下面左图中的绿点表示获得正向奖励的动作,右图表示更新后的策略,可以发现产生正向奖励的区域的概率都增加了(离圆心的距离更近)。
基本概念
对象系统:策略梯度的学习对象,这个对象即可以是一个系统,比如汽车或一个游戏,也可以是一个对手,比如势头剪刀布的游戏对手或者一个职业的围棋手。
Policy(策略):$\pi_\theta(a|s)$ 表示在状态 $s$ 和参数 $\theta$ 条件下发生 $a$ 动作的概率。
Episode(轮次):表示从起始状态开始使用某种策略产生动作与对象系统交互,直到某个终结状态结束。比如在围棋游戏中的一个轮次就是从棋盘中的第一个落子开始直到对弈分出胜负,或者自动驾驶的轮次指从汽车启动一直到顺利抵达指定的目的地,当然撞车或者开进水塘也是种不理想的终结状态。
Trajectory(轨迹 $\tau$ ):表示在 PG 一个轮次的学习中状态 $s$ ,动作 $a$ 和奖励 $r$ 的顺序排列。由于策略产生的是非确定的动作,同一个策略在多个轮次可以产生多个不同的轨迹。$\tau=(s_1, a_1, \dots, s_t, a_t)$
轮次奖励 $\sum r(\tau)$ :表示在一个轮次中依次动作产生的奖励的总和。 因此在实现中对每个策略会求多个轮次的平均值。
策略梯度的学习是一个策略的优化过程,最开始随机的生成一个策略,当然这个策略对对象系统一无所知,所以用这个策略产生的动作会从对象系统那里很可能会得到一个负面奖励,这个过程就好像在PONG游戏中我们对飞来的乒乒球无动于衷而导致对方的得分增加。为了击败对手我们需要逐渐的改变策略,使得本方的比分增加。策略梯度在一轮的学习中使用同一个策略直到该轮结束,通过梯度上升改变策略并开始下一轮学习,如此往复直到轮次累计奖励不再增长停止。
理论推导
首先需要将策略参数话 $\pi(a|s,\theta)=\pi_\theta(a|s)$ ,从轨迹 $\tau$ 中直接找到策略上升的方向,定义这条轨迹在策略 $\pi_\theta$ 下出现的概率为:
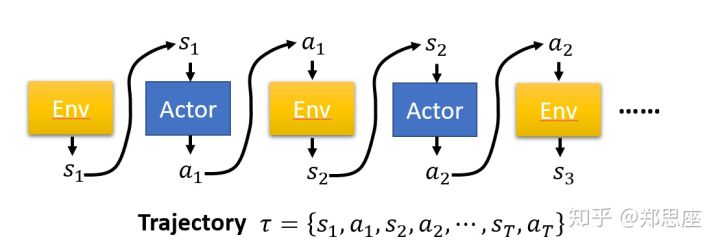
我们需要定义长期汇报 $J(\theta)$ ,目标最大化它。过程如下:

由于 $\nabla_{\theta} J(\theta)$ 无法直接求出,因此采用蒙特卡洛采样法来近似求解。然后根据梯度上升公式更新参数 $\theta$ 直至收敛,流程如下:
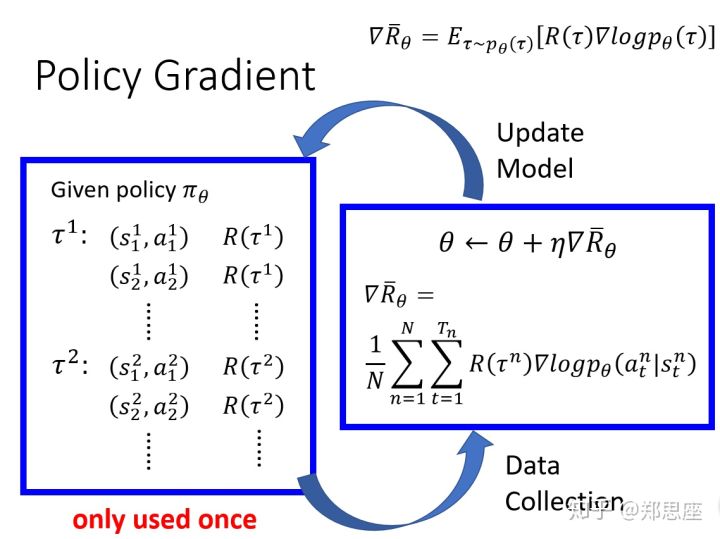
从机器学习的原理的角度来看,策略梯度和传统的监督式学习的学习过程还是比较相似的,每轮次都由前向反馈和反向传播构成,前向反馈负责计算目标函数,反向传播负责更新算法的参数,依此进行多轮次的学习指导学习效果稳定收敛。唯一不同的是,监督式学习的目标函数相对直接,即目标值和真实值的差,这个差值通过一次前向反馈就能得到;而策略梯度的目标函数源自轮次内所有得到的奖励,并且需要进行一定的数学转换才能计算,另外由于用抽样模拟期望,也需要对同一套参数进行多次抽样来增加模拟的准确性。
缺陷及改进
我们把 $R(\tau^n)$ 看作是 $\sum_{t=1}^T \nabla_\theta log \pi_\theta (a_t|s_t)$ 的权重,这样会存在两个问题:
- $R(\tau^n)$ 能始终为正,也就是会导致所有策略都会增强,而我们的初衷是降低表现差的行动的概率,提升表现好的行动的概率。
- $R(\tau^n) = \sum_{t=1}^T r_t$ ,对于序列中的每一时间段的元组 $(s_t, a_t)$ 只能影响 $t$ 时刻之后的回报,不能影响之前的回报。
针对上述两个问题,解决方案如下:
- 引入基线:权重项变为 $R(\tau^n)-b$ ,通常 $b=E[R(\tau^n)]$ ,表示对所有轨迹的累计回报求平均。引入 $b$ 不会对 $\nabla_\theta J(\theta)$ 产生影响,证明如下:
- 减少无效元素:权重项变为 $\sum_{t’=t}^T \gamma^{t’-t}r_t$ ,$\gamma$ 表示衰减系数,该式表示只计算t时刻之后的回报,即未来不影响过去。
综上改进后的式子为 $\nabla_\theta J(\theta) \approx \frac {1} {N} \sum_{n=1}^N [(\sum_{t=1}^T \nabla_\theta log \pi_\theta (a_t^n|s_t^n))(\sum_{t’=t}^T \gamma^{t’-t}r_t^n - b)] $
总结
策略梯度基本靠“猜”。这里的猜不是瞎猜,而是用随机(Stochastic)的方式控制动作的产生进而影响策略的变化,随机既保证了非确定性又能通过控制概率避免完全盲目,是策略梯度解决复杂问题的核心和基础。然而双刃剑的另一面是,”猜“造成了策略梯度方差大、收敛慢的缺点,这是源于策略梯度为了避免遍历所有状态而不得不付出的代价,无法完全避免。 但是瑕不掩瑜,策略梯度除了理论上的处理复杂问题的优势,在实践应用中也有明显的优势,那就是它可以仅靠与目标系统交互进行学习,而不需要标签数据,可以节省了大量的人力。 目前层出不穷的 variance reduction 的方法也证明了人们不仅没有因为策略梯度的缺点放弃它,反而正在通过不断的改进使其扬长避短,发扬光大。