Attention Model

人脑的注意力模型，说到底是一种资源分配模型，在某个特定时刻，你的注意力总是集中在画面中的某个焦点部分，而对其它部分视而不见。Attention Model 被广泛使用在自然语言处理、图像识别及语音识别等各种不同类型的深度学习任务中。

RNN的局限

机器翻译解决的是输入是一串在某种语言中的一句话，输出是目标语言相对应的话的问题，如将德语中的一段话翻译成合适的英语。之前的Neural Machine Translation(NMT)模型中，通常的配置是encoder-decoder结构，即encoder读取输入的句子将其转换为定长的一个向量，然后decoder再将这个向量翻译成对应的目标语言的文字。通常encoder及decoder均采用RNN结构如LSTM或GRU等。如下图所示，我们利用encoder RNN将输入语句信息总结到最后一个hidden vector中，并将其作为decoder初始的hidden vector，利用decoder解码成对应的其他语言中的文字。

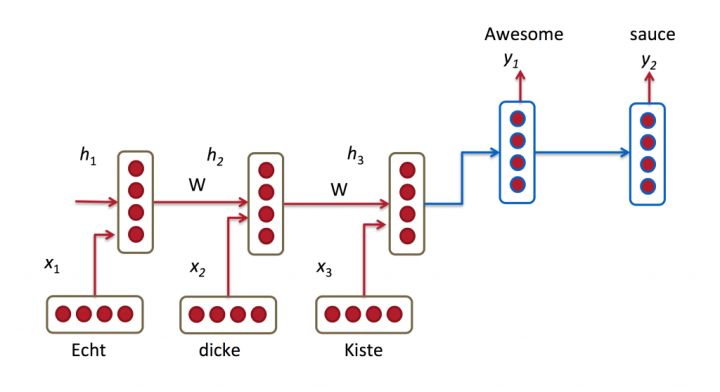
但是这个结构有些问题，尤其是RNN机制实际中存在长程梯度消失或梯度爆炸的问题。对于较长的句子，我们很难寄希望于将输入的序列转化为定长的向量而保存所有的有效信息。所以随着所需翻译句子的长度的增加，这种结构的效果会显著下降。

为了解决这一由长序列到定长向量转化而造成的信息损失的瓶颈，Attention注意力机制被引入了。AM跟人类翻译文章时候的思路有些类似，即将注意力关注于我们翻译部分对应的上下文。在Attention模型中，当我们翻译当前词语时，我们会寻找源语句中相对应的几个词语，并结合之前的已经翻译的部分作出相应的翻译。如下图所示，当我们翻译“knowledge”时，只需将注意力放在源句中“知识”的部分，当翻译“power”时，只需将注意力集中在”力量“。这样，当我们decoder预测目标翻译的时候就可以看到encoder的所有信息，而不仅局限于原来模型中定长的隐藏向量，并且不会丧失长程的信息。

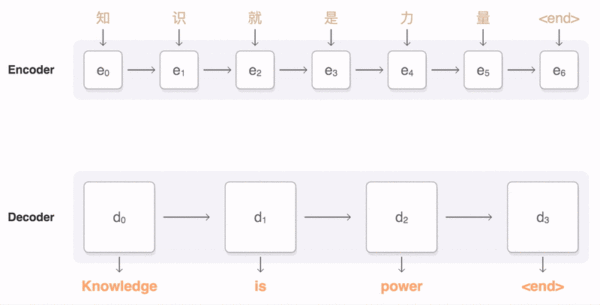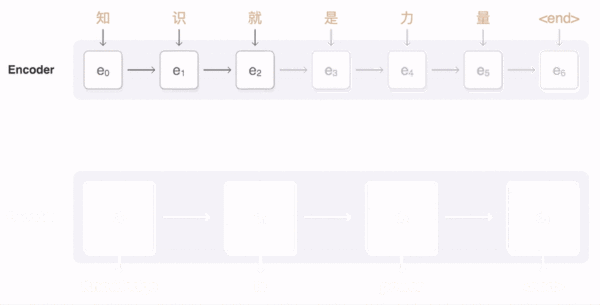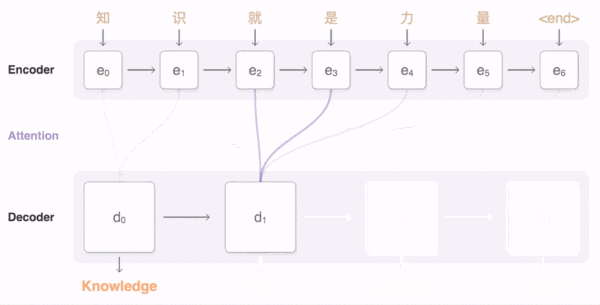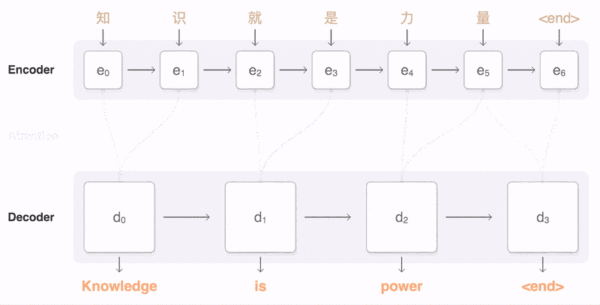
Encoder-Decoder框架

目前绝大部分文献中出现的AM是附着在Encoder-Decoder框架下的，但AM可以看作一种通用的思想，本身并不依赖于Encoder-Decoder。Encoder-Decoder框架可以看作是一种文本处理领域的研究模式，下图是其抽象表示：

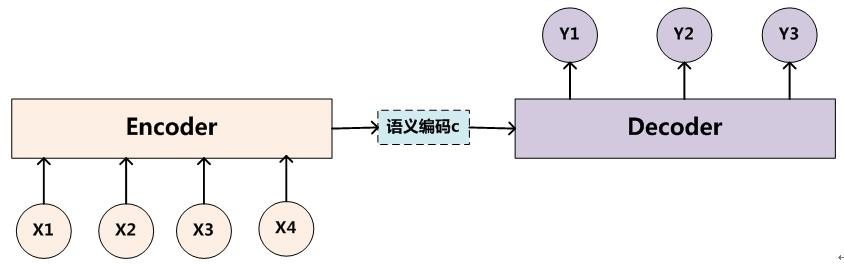
Encoder-Decoder框架可以这么直观地去理解：可以把它看作适合处理由一个句子（或篇章）生成另外一个句子（或篇章）的通用处理模型。对于句子对 $ < X, Y > $（例如 $X$ 是一个问句， $Y$ 是答案； $X$ 是一个句子， $Y$ 是抽取的关系三元组； $X$ 是汉语句子， $Y$ 是汉语句子的英文翻译等等），我们的目标是给定输入句子 $X$ ，期待通过Encoder-Decoder框架来生成目标句子 $Y$ 。 $X$ 和 $Y$ 分别由各自的单词序列构成：

$X = <x_1, x_2, \dots, x_m> \\ Y = <y_1, y_2, \dots, y_n>$

编码器Encoder对输入句子 $X$ 进行编码，将输入句子通过非线性变换转化为中间语义表示 $C$：

$C = \mathcal{F}(x_1, x_2, \dots, x_m)$

解码器Decoder的任务是根据句子 $X$ 的中间语义表示 $C$ 和之前已经生成的历史信息 $y_1, y_2, \dots. y_{i-1}$ 来生成i时刻要生成的单词 $y_i$ ：

$y_i = \mathcal{G}(C, y_1, y_2, \dots, y_{i-1})$

每个 $y_i$ 都依次产生，那么看起来就是整个系统根据输入句子 $X$ 生成了目标句子 $Y$。

以上介绍的Encoder-Decoder模型可以看作是注意力不集中的分心模型。目标句子 $Y$ 中每个单词的生成过程如下：

$\begin{align} y_1 &= \mathcal{G}(C) \\ y_2 &= \mathcal{G}(C, y_1) \\ y_3 &= \mathcal{G}(C, y_1, y_2) \end{align}$

从这里可以看出，在生成目标句子的单词时，不论生成哪个单词，它们使用的语义编码 $C$ 都是一样的，没有任何区别。而语义编码 $C$ 是由句子 $X$ 的每个单词经过Encoder 编码产生的，这意味着不论是生成哪个单词（$y_1, y_2, y_3$），其实句子$X$ 中任意单词对生成某个目标单词 $y_i$ 来说影响力都是相同的，没有任何区别（其实如果Encoder是RNN的话，理论上越是后输入的单词影响越大，并非等权的，估计这也是为何Google提出Sequence to Sequence模型时发现把输入句子逆序输入做翻译效果会更好的小Trick的原因）。这就是为何说这个模型没有体现出注意力的缘由。

引入AM模型，以翻译一个英语句子举例：输入 $X$：Tom chase Jerry。理想输出 $Y$：汤姆追逐杰瑞。

应该在翻译“杰瑞”的时候，体现出英文单词对于翻译当前中文单词不同的影响程度，比如给出类似下面一个概率分布值：

$(Tom, 0.3) \quad (chase, 0.2) \quad (Jerry, 0.5)$

每个英文单词的概率代表了翻译当前单词“杰瑞”时，注意力分配模型分配给不同英文单词的注意力大小。同理，目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。这意味着在生成每个单词 $y_i$ 的时候，原先都是相同的中间语义表示 $C$ 会替换成根据当前生成单词而不断变化的 $C_i$ 。AM模型的关键就是这里，即由固定的中间语义表示 $C$ 换成了根据当前输出单词来调整成加入注意力模型的变化的 $C_i$ 。

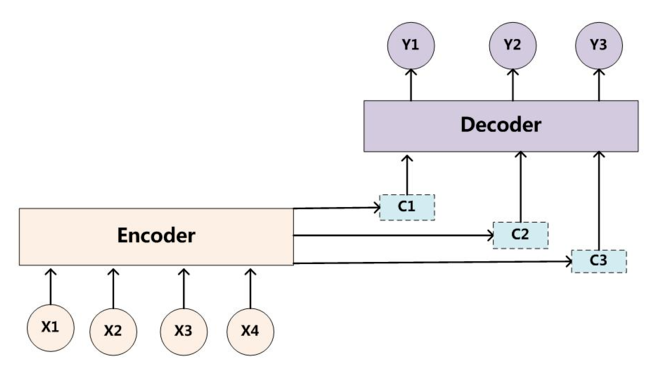
即生成目标句子单词的过程成了下面的形式：

$\begin{align} y_1 &= \mathcal{G}(C_1) \\ y_2 &= \mathcal{G}(C_2, y_1) \\ y_3 &= \mathcal{G}(C_3, y_1, y_2) \end{align}$

而每个 $C_i$ 可能对应着不同的源语句子单词的注意力分配概率分布。比如对于上面的英汉翻译来说，其对应的信息可能如下：

$\begin{align} C_{汤姆} &= g(0.6*f2("Tom"), 0.2*f2(chase), 0.2*f2("Jerry")) \\ C_{追逐} &= g(0.2*f2("Tom"), 0.7*f2(chase), 0.1*f2("Jerry")) \\ C_{杰瑞} &= g(0.3*f2("Tom"), 0.2*f2(chase), 0.5*f2("Jerry")) \\ \end{align}$

其中，$f2$ 函数代表Encoder对输入英文单词的某种变换函数，比如如果Encoder是用的RNN模型的话，这个 $f2$ 函数的结果往往是某个时刻输入 $x_i$ 后隐层节点的状态值；$g$ 代表Encoder根据单词的中间表示合成整个句子中间语义表示的变换函数，一般的做法中，$g$ 函数就是对构成元素加权求和，也就是常常在论文里看到的下列公式：

$C_i = \sum_{j=1}^{T_x} \alpha_{ij}h_j$

假设 $i$ 就是上面的“汤姆”，$T_x$ 为3，代表输入句子的长度，$h1=f2(“Tom”), h2=f2(“Chase”), h3=f2(“Jerry”)$，对应的注意力模型权值分别是$0.6,0.2,0.2$，所以 $g$ 函数就是个加权求和函数。$C_i$ 的形成过程如下图所示：

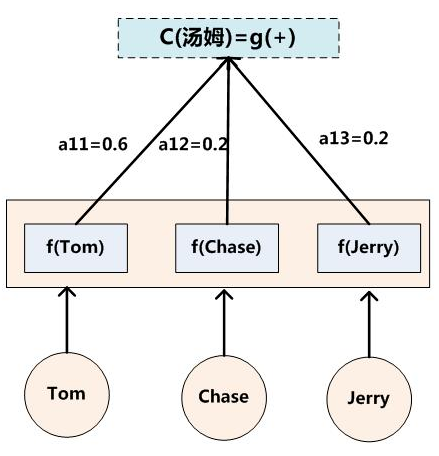
注意力分配概率分布 $(0.6, 0.2, 0.2)$ 怎么求出来的呢？为了便于说明，我们假设对图2的非AM模型的Encoder-Decoder框架进行细化，Encoder采用RNN模型，Decoder也采用RNN模型，则图2的转换为下：

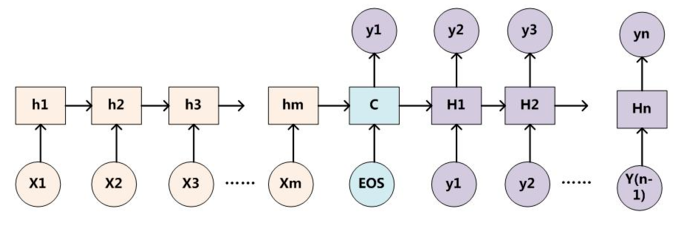
注意力分配概率分布值的通用计算过程：

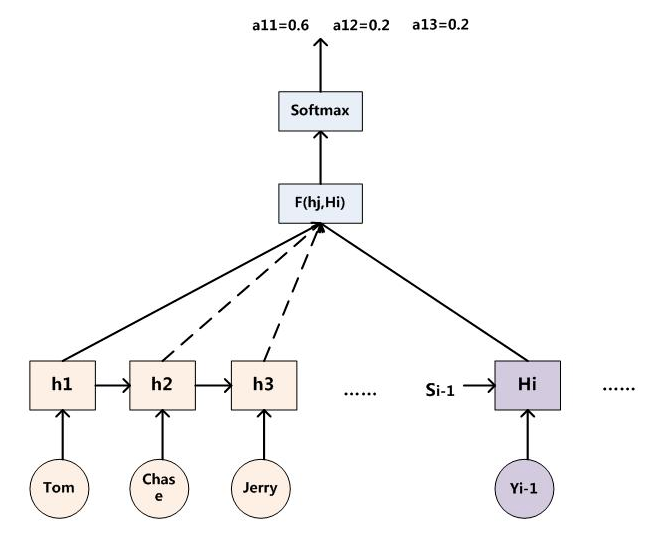
对于采用RNN的Decoder来说，如果要生成 $Y_i$ 单词，在时刻 $i$ ，我们是可以知道在生成 $Y_i$ 之前的隐层节点i时刻的输出值 $H_i$ 的。而我们的目的是要计算生成 $Y_i$ 时的输入句子单词“Tom”、“Chase”、“Jerry”对 $Y_i$ 来说的注意力分配概率分布，那么可以用 $i$ 时刻的隐层节点状态 $H_i$ 去和输入句子中每个单词对应的RNN隐层节点状态 $h_j$ 进行对比，即通过函数 $F(h_j, H_i)$ 来获得目标单词 $Y_i$ 和每个输入单词对应的对齐可能性。这个 $F$ 函数在不同论文里可能会采取不同的方法，然后函数 $F$ 的输出经过Softmax进行归一化就得到了注意力分配概率分布。上图显示的是当输出单词为“汤姆”时刻对应的输入句子单词的对齐概率。绝大多数AM模型都是采取上述的计算框架来计算注意力分配概率分布信息，区别只是在 $F$ 的定义上可能有所不同。

数学表达

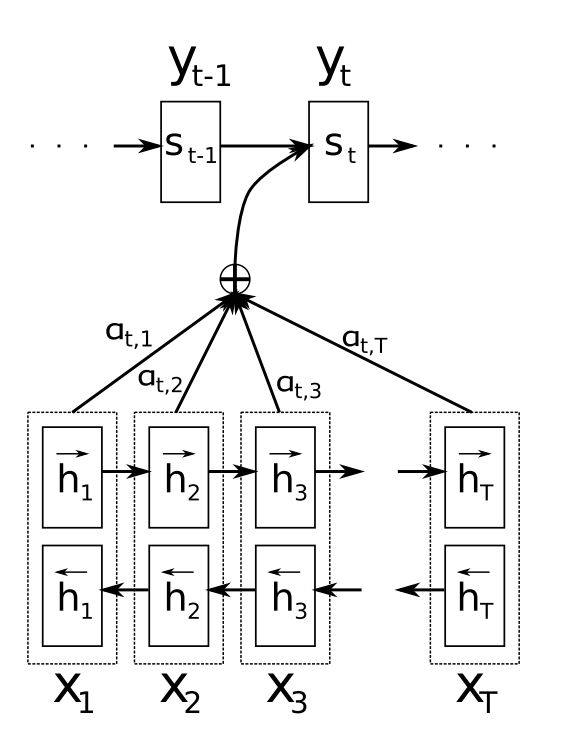
我们首先利用RNN结构得到encoder的hidden state $(h_1, h_2, \dots, h_T)$
假设当前decoder的hidden state 是 $s_{t-1}$，我们可以计算每一个输入位置 $j$ 与当前输出位置的关联性，$e_{tj} = a(s_{t-1}, h_j)$ ，写成相应的向量形式即为 $\vec {e_t} = (a(s_{t-1}, h_1), a(s_{t-1}, h_2), \dots. a(s_{t-1}, h_T))$
对 $\vec {e_t}$ 进行softmax操作得到attention的分布。$\vec {\alpha_t} = softmax(\vec {e_t})$，展开形式为 $\alpha_{tj} = \frac {e^{e_{tj}}} {\sum_{k=1}^T e^{e_{tk}}}$
利用 $\vec {\alpha_t}$ 进行加权求和得到相应的context vector $\vec {c_t} = \sum_{j=1}^T \alpha_{tj}hj$
由此，我们可以计算decoder的下一个hidden state $s_t = f(s_{t-1}, y_{t-1}, c_t)$ 以及该位置的输出 $p(y_t | y_1, \dots, y_{t-1}, \vec x) = g(y_{i-1}, s_t, c_t)$

物理含义

上述内容就是论文里面常常提到的Soft Attention Model（任何单词都会给一个权值，没有筛选条件）的基本思想。那么怎么理解AM模型的物理含义呢？一般文献里会把AM模型看作是单词对齐模型，这是非常有道理的。目标句子生成的每个单词对应输入句子单词的概率分布可以理解为输入句子单词和这个目标生成单词的对齐概率，这在机器翻译语境下是非常直观的：传统的统计机器翻译一般在做的过程中会专门有一个短语对齐的步骤，而注意力模型其实起的是相同的作用。在其他应用里面把AM模型理解成输入句子和目标句子单词之间的对齐概率也是很顺畅的想法。

本质思想

如果把Attention机制从上文讲述例子中的Encoder-Decoder框架中剥离，并进一步做抽象，可以更容易看懂Attention机制的本质思想。

将Source中的构成元素想象成是由一系列的数据对构成，此时给定Target中的某个元素Query($H_i$)，通过计算Query和各个Key的相似性或者相关性，得到每个Key对应Value的权重系数，然后对Value进行加权求和，即得到了最终的Attention数值。所以本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。即可以将其本质思想改写为如下公式：

$Attention(Query, Source) = \sum_{i=1}^{L_x} Similarity(Query, Key_i) * Value_i$

$Lx$ 表示 Source 的长度，如一句话中单词的个数。上文所举的机器翻译的例子里，因为在计算Attention的过程中，Source中的Key和Value合二为一，指向的是同一个东西($h_i = f2$)，也即输入句子中每个单词对应的语义编码，所以可能不容易看出这种能够体现本质思想的结构。

从概念上理解，把Attention仍然理解为从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上，忽略大多不重要的信息，这种思路仍然成立。聚焦的过程体现在权重系数的计算上，权重越大越聚焦于其对应的Value值上，即权重代表了信息的重要性，而Value是其对应的信息。

从图9可以引出另外一种理解，也可以将Attention机制看作一种软寻址（Soft Addressing）:Source可以看作存储器内存储的内容，元素由地址Key和值Value组成，当前有个Key=Query的查询，目的是取出存储器中对应的Value值，即Attention数值。通过Query和存储器内元素Key的地址进行相似性比较来寻址，之所以说是软寻址，指的不像一般寻址只从存储内容里面找出一条内容，而是可能从每个Key地址都会取出内容，取出内容的重要性根据Query和Key的相似性来决定，之后对Value进行加权求和，这样就可以取出最终的Value值，也即Attention值。所以不少研究人员将Attention机制看作软寻址的一种特例，这也是非常有道理的。

AM的具体计算过程如下：

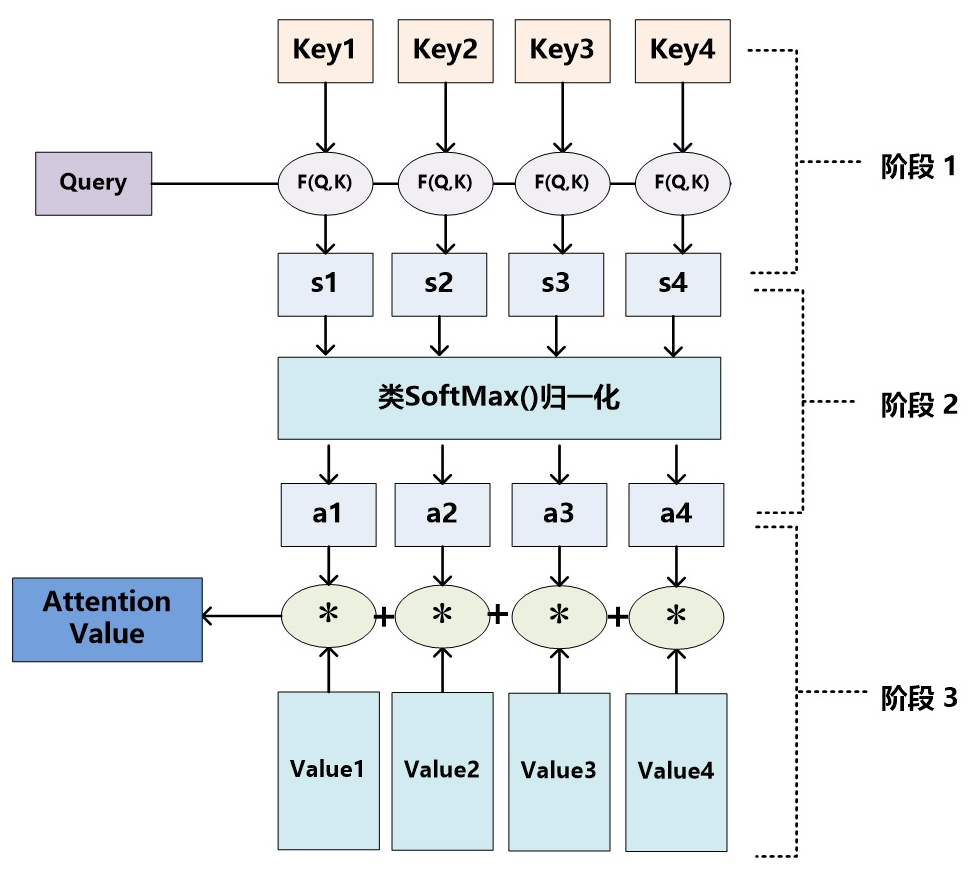
Query和Key的相似性计算有如下常用几种方法：

点积：$Query \ast Key_i$
cosine：$\frac { Query \ast key_i } { | Query | \ast | Key_i | }$
多层感知器：$MLP(Query, Key_i)$
欧式距离：$\sum_{j=1}^n (Query_j - Key_{ij})^2$