
误差反向传播算法简称反向传播算法(Back Propagation)。使用反向传播算法的多层感知器又称为BP神经网络。
BP算法是一个迭代算法,它的基本思想如下:
- 将训练集数据输入到神经网络的输入层,经过隐藏层,最后达到输出层并输出结果,这就是前向传播过程。
- 由于神经网络的输出结果与实际结果有误差,则计算估计值与实际值之间的误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层;
- 在反向传播的过程中,根据误差调整各种参数的值(相连神经元的权重),使得总损失函数减小。
- 迭代上述三个步骤(即对数据进行反复训练),直到满足停止准则。
示例
有如下一个神经网络:
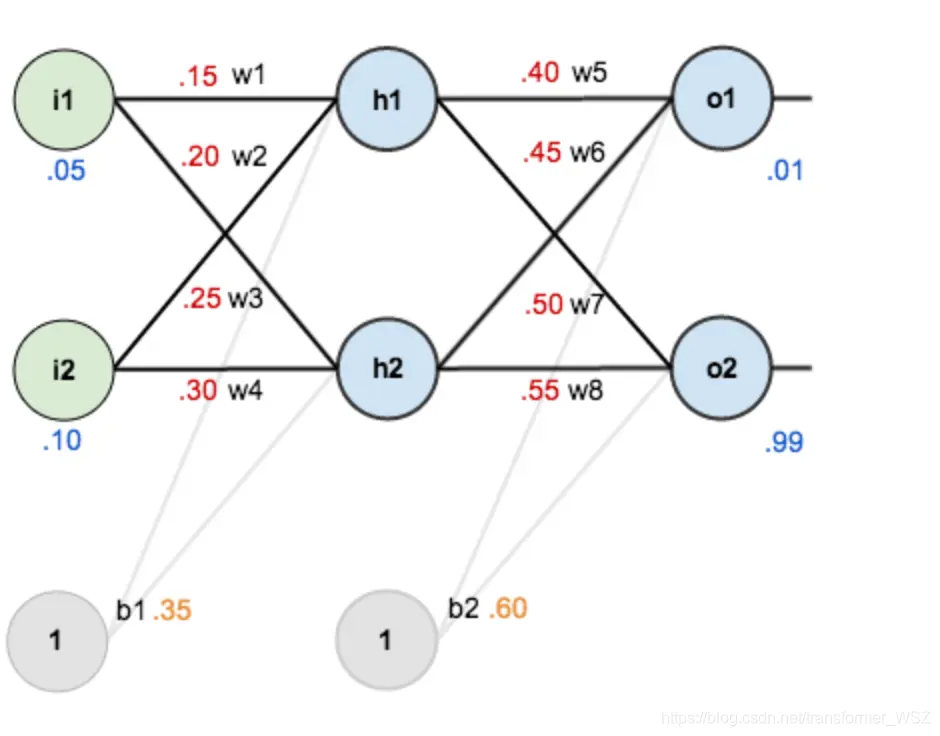
第一层是输入层,包含两个神经元 $i_1$,$i_2$ 和偏置项 $b_1$;第二层是隐藏层,包含两个神经元 $h_1$,$h_2$ 和偏置项 $b_2$;第三层是输出 $o_1$,$o_2$。每条线上标的 $w_i$ 是层与层之间连接的权重。激活函数是 $sigmod$ 函数。我们用 $z$ 表示某神经元的加权输入和;用 $a$ 表示某神经元的输出。
上述各参数赋值如下:
| 参数 | 值 |
|---|---|
| $i_1$ | 0.05 |
| $i_2$ | 0.10 |
| $w_1$ | 0.15 |
| $w_2$ | 0.20 |
| $w_3$ | 0.25 |
| $w_4$ | 0.30 |
| $w_5$ | 0.40 |
| $w_6$ | 0.45 |
| $w_7$ | 0.50 |
| $w_8$ | 0.55 |
| $b_1$ | 0.35 |
| $b_2$ | 0.60 |
| $o_1$ | 0.01 |
| $o_2$ | 0.99 |
Step 1 前向传播
输入层 —-> 隐藏层
神经元 $h_1$ 的输入加权和:
神经元 $h_1$ 的输出 $a_{h1}$ :
同理可得,神经元 $h_2$ 的输出 $a_{h2}$ :
隐藏层 —-> 输出层
计算输出层神经元 $o1$ 和 $o2$ 的值:
前向传播的过程就结束了,我们得到的输出值是 $[0.751365069, 0.772928465]$ ,与实际值 $[0.01, 0.99]$ 相差还很远。接下来我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
- 计算损失函数:
但是有两个输出,所以分别计算 $o_1$ 和 $o_2$ 的损失值,总误差为两者之和:
- 隐藏层 —-> 输出层的权值更新
以权重参数 $w_5$ 为例,如果我们想知道 $w_5$ 对整体损失产生了多少影响,可以用整体损失对 $w_5$ 求偏导:
下面的图可以更直观了解误差是如何反向传播的:
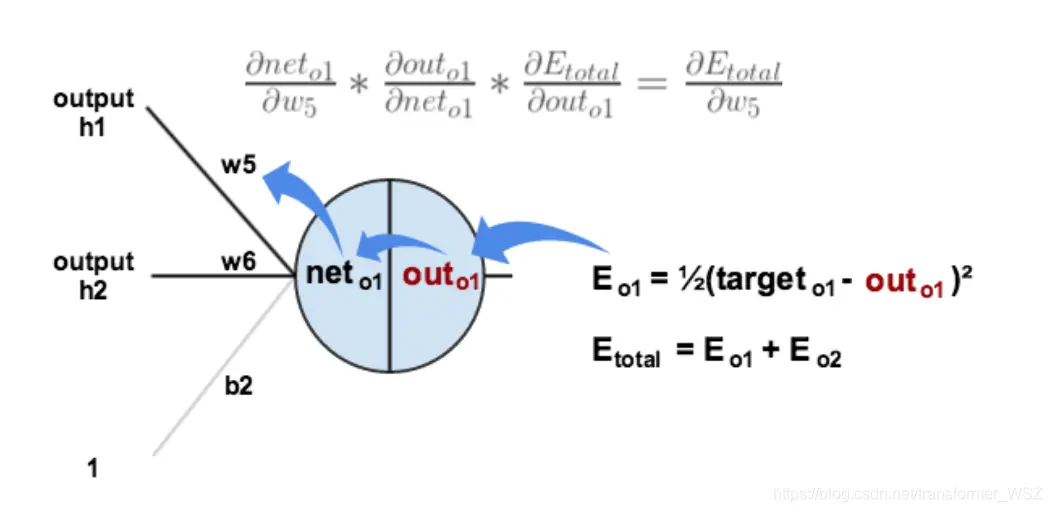
我们现在分别来计算每个式子的值:
计算 $\frac {\partial E_{total}} {\partial a_{o_1}}$ :
计算 $\frac {\partial E_{total}} {\partial a_{o_1}}$ :
计算 $\frac {\partial z_{o_1}} {\partial w_5}$ :
最后三者相乘:
这样我们就算出整体损失 $E_{total}$ 对 $w_5$ 的偏导值。
针对上述公式,为了表达方便,使用 $\delta_{o_1}$ 来表示输出层的误差:
因此整体损失 $E_{total}$ 对 $w_5$ 的偏导值可以表示为:
最后我们来更新 $w_5$ 的值:
同理可更新 $w_6, w_7, w_8$ :
- 隐藏层 —-> 隐藏层的权值更新:
计算 $\frac {\partial E_{total}} {\partial w_1}$ 与上述方法类似,但需要注意下图:
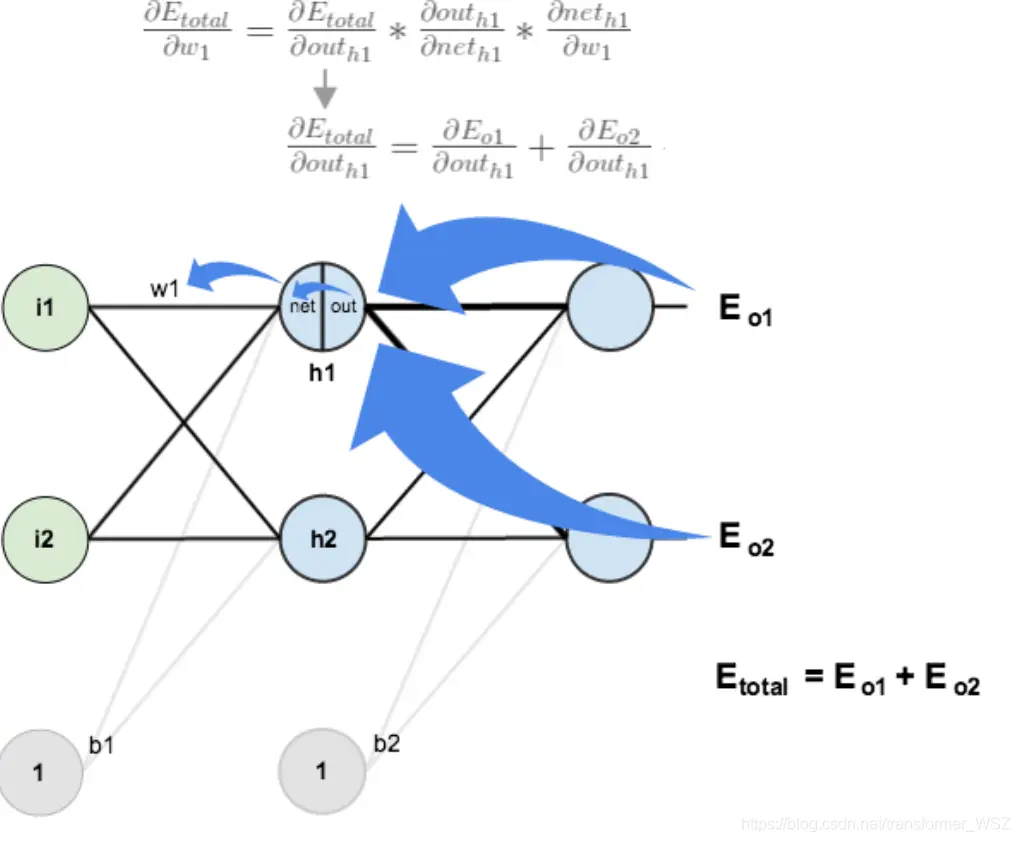
计算 $\frac {\partial E_{total}} {\partial a_{h_1}}$ :
先计算 $\frac {\partial E_{o_1}} {\partial a_{h_1}}$ :
同理可得:
两者相加得:
计算 $\frac {a_{h_1}} {z_{h_1}}$ :
计算 $\frac {\partial z_{h_1}} {\partial w_1}$
最后三者相互乘:
为了简化公式,用 $\delta_{h_1}$ 表示隐藏层单元 $h_1$ 的误差:
最后更新 $w_1$ 的权值:
同理,更新 $w_2, w_3, w_4$ 权值:
这样,反向传播算法就完成了,最后我们再把更新的权值重新计算,不停地迭代。在这个例子中第一次迭代之后,总误差 $E_{total}$ 由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为$[0.015912196,0.984065734](原输入为[0.01,0.99]$ ,证明效果还是不错的。
公式推导
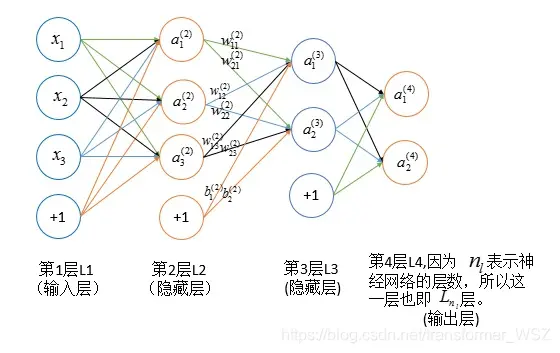
符号说明
| 符号 | 说明 |
|---|---|
| $n_l$ | 网络层数 |
| $y_j$ | 输出层第 $j$ 类标签 |
| $S_l$ | 第 $l$ 层神经元个数(不包括偏置项) |
| $g(x)$ | 激活函数 |
| $w_{ij}^{l}$ | 第 $l-1$ 层的第 $j$ 个神经元连接到第 $l$ 层第 $i$ 个神经元的权重 |
| $b_i^{l}$ | 第 $l$ 层的第 $i$ 个神经元的偏置 |
| $z_i^{l}$ | 第 $l$ 层的第 $i$ 个神经元的输入加权和 |
| $a_i^{l}$ | 第 $l$ 层的第 $i$ 个神经元的输出(激活值) |
| $\delta_i^{l}$ | 第 $l$ 层的第 $i$ 个神经元产生的错误 |
推导过程
基本公式
梯度方向传播公式推导
初始条件
以一个输入样本为例:
递推公式
反向传播伪代码
- 输入训练集。
- 对于训练集的每个样本 $\vec x$ ,设输入层对应的激活值为 $a^l$ :
- 前向传播:$z^l = w^l*a^{l-1}+b^l, a^l = g(z^l)$
- 计算输出层产生的误差:$\delta^L = \frac {\partial J(\theta)} {\partial a^L} \odot g’(z^L)$
- 反向传播错误:$\delta^l = ((w^{l+1})^T*\delta^{l+1}) \odot g’(z^l)$
- 使用梯度下降训练参数:
- $w^l \dashrightarrow w^l - \frac {\alpha} {m} \sum_x\delta^{x, l}*(a^{x, l-1})^T$
- $b^l \dashrightarrow b^l - \frac {\eta} {m} \sum_x\delta^{x, l}$
交叉熵损失函数推导
对于多分类问题,$softmax$ 函数可以将神经网络的输出变成一个概率分布。它只是一个额外的处理层,下图展示了加上了 $softmax$ 回归的神经网络结构图:
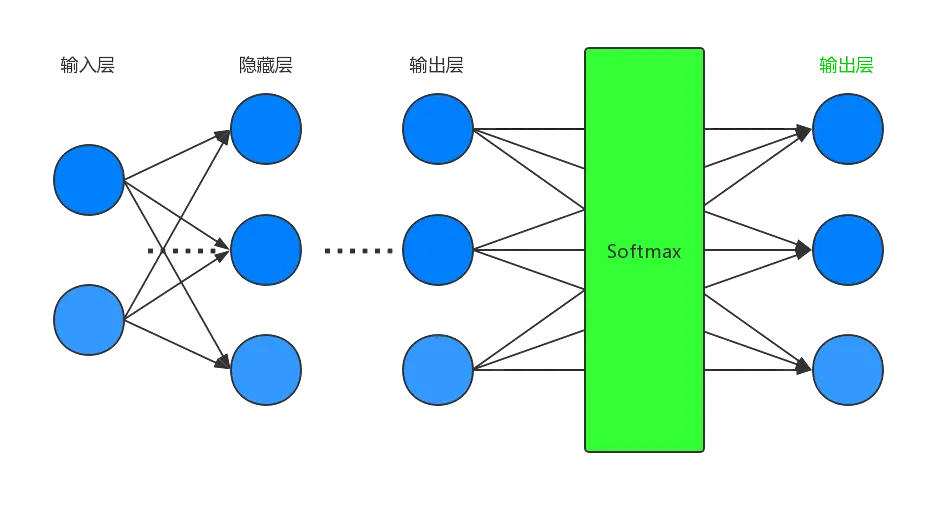
递推公式仍然和上述递推公式保持一致。初始条件如下:
$softmax$ 偏导数计算:
推导过程
由上可知:
$\therefore$ 反向传播选代算法的初始值为: